Парадокс Бертрана — проблема в классической интерпретации по теории вероятностей. Джозеф представил его в своей работе Calcul des probabilités (1889) в качестве примера, что вероятности не могут быть четко определены, если механизм или метод производят случайную переменную.
Постановка проблемы
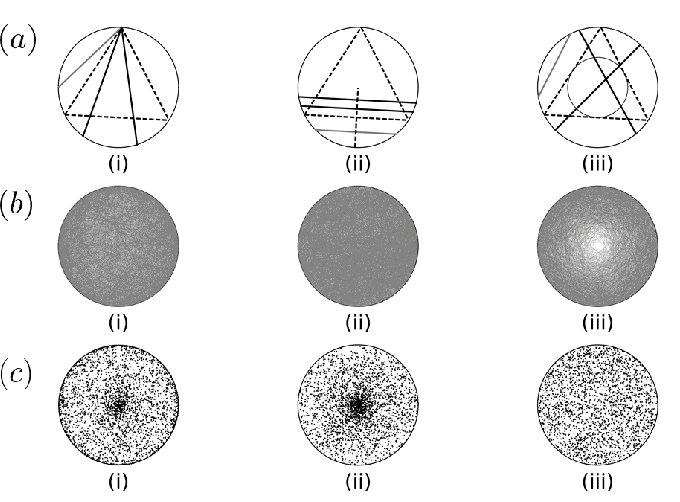
Парадокс Бертрана состоит в следующем.
Для начала необходимо рассмотреть равносторонний треугольник, вписанный в круг. При этом диаметр выбран случайным образом. Какова вероятность того, что она длиннее стороны треугольника?
 Вам будет интересно:Иномарки в СССР: фото моделей
Вам будет интересно:Иномарки в СССР: фото моделей
Бертран привел три аргумента, все они, по-видимому, верны, но дали разные результаты.
Метод «случайных конечных точек»
Необходимо выбрать два места на окружности и нарисовать дугу, соединяющую их. Для расчета рассматривается парадокс вероятности Бертрана. Необходимо представить, что треугольник повернут так, что его вершина совпадает с одной из конечных точек хорды. Стоит обратить внимание, что, если другая часть находится на дуге между двумя местами, окружность длиннее стороны треугольника. Длина дуги одна треть окружности, поэтому вероятность того, что случайная хорда продолжительнее, равна 1/3.
Метод выбора
 Вам будет интересно:«Ко скольки» как пишется? Да никак не пишется, потому что нет такого слова!
Вам будет интересно:«Ко скольки» как пишется? Да никак не пишется, потому что нет такого слова!
Необходимо выбрать радиус круга и точку на нем. После этого нужно построить аккорд через это место, перпендикулярно диаметру. Чтобы вычислить рассматриваемый парадокс Бертрана теории вероятности, нужно представить, что треугольник повернут так, что сторона перпендикулярна радиусу. Хорда длиннее катета, если выбранная точка находится ближе к центру круга. И в этом случае сторона треугольника делит пополам радиус. Поэтому вероятность, что хорда длиннее стороны вписанной фигуры, равна 1/2.
Случайные аккорды
Метод средней точки. Необходимо выбрать место на круге и создать аккорд с заданной серединой. Ось продолжительнее края вписанного треугольника, в случае, если подобранное место находится в пределах концентрической окружности радиуса 1/2. Площадь меньшего круга является одной четвертой большей фигуры. Поэтому вероятностью случайной хорды длиннее, чем сторона вписанного треугольника, и равна 1/4.
Как представлено выше, методы выбора отличаются по весу, который они дают определенным аккордам, которые являются диаметрами. В методе 1 каждый аккорд может быть выбран точно одним способом, независимо от того, является ли он диаметром.
 Вам будет интересно:Бирон Эрнст Иоганн - фаворит русской императрицы Анны Иоанновны, герцог Курляндии и Семигалии: биография, мифы и правда
Вам будет интересно:Бирон Эрнст Иоганн - фаворит русской императрицы Анны Иоанновны, герцог Курляндии и Семигалии: биография, мифы и правда
В методе 2, каждая прямая линия может быть выбрана двумя способами. Тогда как любой другой аккорд будет избираться только одной из возможностей.
В методе 3 каждому выбору средней точки соответствует единственный параметр. За исключением центра круга, который является серединой всех диаметров. Этих проблем можно избежать, «упорядочив» все вопросы, чтобы исключить параметры, не влияя на результирующие вероятности.
Методы выбора также могут быть визуализированы следующим образом. Аккорд, который не является диаметром, однозначно идентифицируется по его средней точке. Каждый из трех методов выбора, представленных выше, дает различное распределение середины. А 1 и 2 варианты предоставляют два разных неоднородных разделения, в то время, как метод 3 дает равномерное распределение.
Классический парадокс решения проблемы Бертрана зависит от метода, которым аккорд выбирается «наугад». Оказывается, что, если заранее указан способ случайного отбора, задача имеет четко определенное решение. Это связано с тем, что у каждого отдельного метода свое распределение аккордов. Три постановления, продемонстрированные Бертраном, отвечают разным способам отбора и при отсутствии дополнительной информации нет оснований отдавать предпочтение одному над другим. Соответственно, заявленная проблема не имеет единственного решения.
Пример того, как сделать общий ответ уникальным состоит в том, чтобы указать, что конечные точки хорды равномерно распределены между 0 и c, где c - окружность круга. Это распределение такое же, что и в первом аргументе Бертрана, и полученная уникальная вероятность будет 1/3.
Этот парадокс Бертрана Рассела и другие уникальности классической интерпретации возможности оправдывают более строгие формулировки. Включая частоту вероятности и субъективистскую байесовскую теорию.
Что лежит в основе парадокса Бертрана

В своей статье 1973 года «Хорошо поставленная проблема» Эдвин Джейнс предложил свое уникальное решение. Он отметил, что в основе парадокса Бертрана лежит предпосылка, основанная на принципе «максимального невежества». Это значит, что не следует использовать какую-либо информацию, которая не приводится в формулировке проблем. Джейнс указал, что задача Бертрана не определяет положение или размер круга. И утверждал, что поэтому любое определенное и объективное решение должно быть «безразличным» к размеру и положению.
Для иллюстрации
 Вам будет интересно:Задание несложное - загадки про ножницы
Вам будет интересно:Задание несложное - загадки про ножницы
Стоит предположить, что все аккорды наложены случайным образом на круг диаметром 2 сантиметра, теперь необходимо бросать в него соломинки издалека.
Затем нужно взять другой круг с меньшим диаметром (например, 1 сантиметр), который укладывается в большую фигуру. Тогда распределение аккордов на этом меньшем круге должно быть таким же, как на максимальном. Если вторая фигура также перемещается внутри первой, вероятность, в принципе, не должна меняться. Очень легко увидеть, что для метода 3 произойдет следующее изменение: распределение аккордов на маленьком красном круге будет качественно отличаться от разделения на большой окружности.
То же самое происходит для метода 1. Хотя это и труднее увидеть в графическом представлении.
Метод 2 является единственным, который оказывается одновременно масштабным и трансляционным инвариантом.
Способ под номером 3 представляется просто расширяемым.
А вот метод 1 не является ни тем, ни другим.
Тем не менее Джейнс непросто использовал инварианты, чтобы принять или отклонить данные способы. Это оставило бы возможность того, что есть еще один неописанный метод, который бы соответствовал его аспектам разумного значения. Джейнс применял интегральные уравнения, описывающие инвариантности. Чтобы непосредственно определить распределение вероятностей. В его задаче интегральные уравнения действительно имеют единственное решение, и это именно то, что выше было названо вторым методом случайного радиуса.
В статье за 2015 год Алон Дрори утверждает, что принцип Джейнса также может дать два других решения Бертранда. Автор уверяет, что математическая реализация вышеупомянутых свойств инвариантности не уникальна, а зависит от базовой процедуры случайного выбора, которую человек решил использовать. Он показывает, что каждое из трех решений Бертрана может быть получено с применением вращательной, масштабирующей и поступательной инвариантности. При этом заключая, что принцип Джейнса так же подвержен интерпретации, как и сам способ безразличия.
Физические эксперименты

Метод 2 является единственным решением, которое удовлетворяет инвариантам преобразований, которые присутствуют в конкретных физиологических концепциях, таких как статистическая механика и структура газа. А также в предложенном Джейнсом эксперименте по выбрасыванию соломинок с небольшого круга.
Тем не менее можно разработать другие практические эксперименты, которые дают ответы в соответствии с иными способами. Например, чтобы прийти к решению первого метода случайных конечных точек, можно прикрепить счетчик к центру области. И позволить итогам двух самостоятельных вращений выделить окончательные места хорды. Чтобы прийти к решению третьего метода, можно покрыть круг, например, патокой и отметить первую точку, на которую приземляется муха, как среднюю хорды. Несколько созерцателей создали исследования с целью извлечения разных заключений и подтвердили результаты эмпирически.
Последние события
В своей статье 2007 года «Парадокс Бертрана и принцип безразличия» Николас Шакель утверждает, что спустя более столетия задача все еще остается неразрешенной. Она продолжает опровергать принцип безразличия. Кроме того, в своей статье 2013 года «Пересмотрен парадокс Бертрана Рассела: почему все решения неприменимы на практике», Даррелл Р. Роботтом показывает, что все предложенные постановления никак не относятся к его собственному вопросу. Так что оказалось, что парадокс будет гораздо сложнее решить, чем предполагалось ранее.
Шакель подчеркивает, что до сих пор многие ученые и далекие от науки люди пытались разрешить парадокс Бертрана. Преодолевается он все так же с помощью двух разных подходов.
Те, в которых рассматривалось различие между неэквивалентными проблемами, и те, в которых задача все время считалась корректной. Шакель в своих книгах цитирует Луи Мариноффа (как типичного представителя стратегии разграничения) и Эдвина Джейнса (как автора хорошо продуманной теории).
Тем не менее в недавней работе «Решение сложной проблемы» Дидерик Аертс и Массимилиано Сассоли де Бьянки считают, что для решения парадокса Бертрана, предпосылки необходимо искать в смешанной стратегии. Согласно этим авторам, сначала нужного устранить проблему, четко указав природу сущности, которая подвергается рандомизации. И только после того, как это будет сделано, любая задача может считаться корректной. Именно так считает Джейнс.
Так что принцип максимального невежества может быть использован для ее решения. С этой целью, и поскольку проблема не определяет, как должен быть выбран аккорд, принцип применяется не на уровне различных возможных вариантов, а на гораздо более глубоком.
Выборка частей

Эта часть в задаче требует расчета мета-среднего по всем возможным способам, которые авторы называют универсальным средним. Чтобы справиться с этим, они используют метод дискретизации. Вдохновленный тем, что делается в определении закона вероятности в винеровских процессах. Полученный ими результат согласуется с численным следствием Джейнса, хотя их хорошо поставленная задача отличается от первоначальной, авторской.
В экономике и коммерции, парадокс Бертрана, названный в честь его создателя Джозефа Бертрана, описывает ситуацию, в которой два игрока (фирмы) достигают состояния равновесия Нэша. Когда оба предприятия устанавливают цену, равную предельным издержкам (МС).
В основе парадокса Бертрана лежит предпосылка. Она заключается в том, что в таких моделях, как конкуренция Курно, увеличение числа фирм связано со сближением цен с предельными издержками. В этих альтернативных моделях парадокс Бертрана находится в олигополии небольшого количества фирм, которые получают положительную прибыль, взимая цены выше себестоимости.
 Вам будет интересно:Династия Гогенцоллернов: исторические факты, фото
Вам будет интересно:Династия Гогенцоллернов: исторические факты, фото
Для начала стоит предположить, что две фирмы A и B продают однородный товар, каждая из которых имеет одинаковую стоимость производства и распределения. Из этого следует, что покупатели выбирают товар, исключительно исходя из цены. А это значит, что спрос бесконечно эластичен по стоимости. Ни А, ни В не будут устанавливать более высокую цену, чем другие, потому что это приведет к тому, что весь парадокс Бертрана рухнет. Один из участников рынка уступит своему конкуренту. Если они установят одинаковую цену, компании будут разделять прибыль.
С другой стороны, если какая-либо фирма хотя бы немного снизит свою цену, она получит весь рынок и существенно большую отдачу. Поскольку A и B знают об этом, каждый из них будет пытаться подрезать конкурента, пока продукт не будет продаваться с нулевой экономической прибылью.
Недавняя работа показала, что может существовать дополнительное равновесие в парадоксе Бертрана со смешанной стратегией, с положительной экономической прибылью при условии, что монопольная сумма бесконечна. Для случая конечной прибыли было показано, что положительная прибавка в условиях ценовой конкуренции невозможна в смешанных равновесиях и даже в более общем случае коррелированных систем.
На самом деле парадокс Бертрана в экономике редко встречается на практике, потому что реальные продукты почти всегда дифференцируются каким-либо иным образом, кроме цены (например, переплата за лейбл). Фирмы имеют ограничения на свои возможности по производству и распространению. Именно поэтому два предприятия редко имеют одинаковые затраты.
Результат Бертрана парадоксален, потому что, если число фирм увеличивается от одной до двух, цена снижается от монопольной до конкурентной и остается на том же уровне, что и число предприятий, увеличивающихся в дальнейшем. Это не очень реалистично, поскольку в действительности рынки с небольшим количеством фирм, обладающих рыночной властью, обычно устанавливают цену, превышающую предельные издержки. Эмпирический анализ показывает, что в большинстве отраслей с двумя конкурентами получаются положительные прибыли.
В современном мире ученые пытаются найти решения парадокса, которые в большей степени соответствуют модели конкуренции Курно. Где две фирмы на рынке получают положительную прибыль, которая находится где-то между совершенно конкурентным и монопольным уровнями.
Некоторые причины, по которым парадокс Бертран не имеет прямого отношения к экономике:
- Ограничения емкости. Иногда фирмы не имеют достаточных возможностей для удовлетворения всего спроса. Этот момент был впервые поднят Фрэнсисом Эджвортом и дал начало модели Бертрана-Эджворта.
- Целочисленные цены. Цены выше MC исключены, потому что одна фирма может подрезать другую на произвольно небольшую сумму. Если цены являются дискретными (например, должны принимать целочисленные значения), то одна фирма должна подрезать другую не менее чем на один рубль. Это подразумевает, что стоимость на мелкую валюту выше MC. Если же другая фирма устанавливает цену на нее выше, другое предприятие может снизить ее и захватить весь рынок, парадокс Бертрана состоит именно в этом. Это не принесет ей никакой прибыли. Это предприятие предпочтет поделиться продажами 50/50 с другой фирмой и получать сугубо положительную выручку.
- Дифференциация продуктов. Если товары разных фирм отличаются друг от друга, то потребители могут не полностью переключаться на продукты с более низкой ценой.
- Динамичная конкуренция. Повторное взаимодействие или неоднократное ценовое соперничество может привести к равновесию стоимости.
- Больше товара за более высокую сумму. Это следует из повторяющегося взаимодействия. Если одна компания устанавливает свою цену немного выше, она все равно будет получать примерно одинаковое количество покупок, но большую прибыль за каждый товар. Поэтому другая компания будет повышать свою наценку и т. д. (Только в повторных играх, в противном случае динамика идет в другом направлении).
Олигополия

Если две компании могут договориться о цене, то в их долгосрочных интересах сохранить соглашение: доход от снижения стоимости менее чем в два раза превышает выручку от соблюдения соглашения и длится только до тех пор, пока другая фирма не снизит свои собственные цены.
Теория вероятностей (как и остальная часть математики) на самом деле является недавним изобретением. И развитие не было гладким. Первые попытки формализовать исчисление вероятности были сделаны Маркизом де Лапласом, который предложил определить понятие как отношение числа событий, приводящих к исходу.
Это, конечно, имеет смысл только в том случае, если число всех возможных мероприятий конечно. И, кроме того, все события равновероятны.
Таким образом, в то время данные понятия, казалось, не имели прочного основания. Попытки распространить определение на случай бесконечного числа событий привели к еще большим трудностям. Парадокс Бертрана является одним из таких открытий, которое заставило математиков настороженно относиться ко всему понятию вероятности.
