Плоскость, наряду с точкой и прямой линией, является базовым геометрическим элементом. С его использованием строятся многие фигуры в пространственной геометрии. В данной статье рассмотрим подробнее вопрос о том, как между двумя плоскостями угол найти.
Понятие
Прежде чем говорить об угле между двумя плоскостями, следует хорошо разобраться, о каком элементе в геометрии пойдет речь. Разберемся в терминологии. Плоскость представляет собой нескончаемую совокупность точек в пространстве, соединяя между собой которые, мы получим вектора. Последние будут по отношению к некоторому одному вектору перпендикулярны. Его принято называть нормалью к плоскости.
 Вам будет интересно:Физика строения вещества. Открытия. Эксперименты. Расчеты
Вам будет интересно:Физика строения вещества. Открытия. Эксперименты. Расчеты
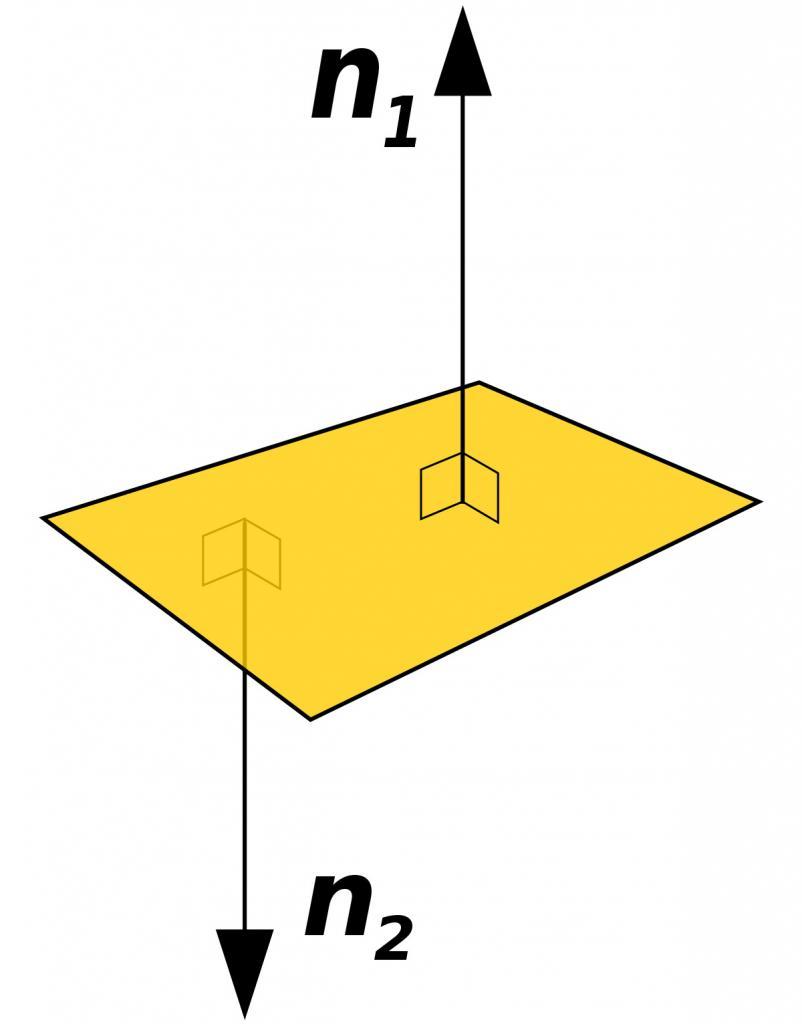
На рисунке выше показана плоскость и два нормальных вектора к ней. Видно, что лежат на одной прямой оба вектора. Угол между ними составляет 180o.
Уравнения
Между двумя плоскостями угол можно определить, если известно математическое уравнение рассматриваемого геометрического элемента. Существует несколько видов подобных уравнений, названия которых перечислены ниже:
- общего типа;
- векторное;
- в отрезках.
Эти три вида являются наиболее удобными при решении различного рода задач, поэтому они чаще всего используются.
Уравнение общего типа выглядит следующим образом:
A*x + B*y + C*z + D = 0.
Здесь x, y, z - координаты произвольной точки, принадлежащей данной плоскости. Параметры A, B, C и D представляют собой числа. Удобство этой формы записи заключается в том, что числа A, B, C являются координатами нормального к плоскости вектора.
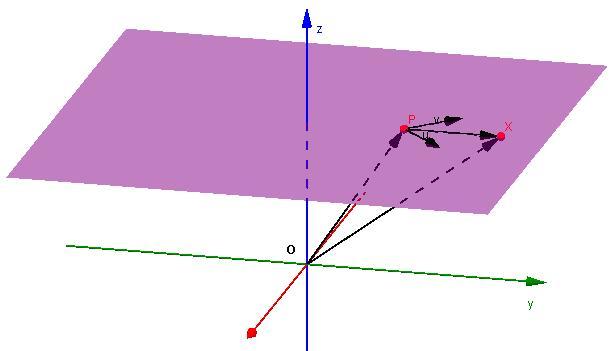
Векторная форма записи плоскости может быть представлена следующим образом:
x, y, z) = (x0, y0, z0) + α*(a1, b1, c1) + β*(a2, b2, c2).
Здесь (a2, b2, c2) и (a1, b1, c1) - параметры двух векторов координаты, которые принадлежат рассматриваемой плоскости. Точка (x0, y0, z0) также лежит в этой плоскости. Параметры α и β могут принимать независимые друг от друга и произвольные значения.
Наконец, уравнение плоскости в отрезках представляют в следующем математическом виде:
x/p + y/q + z/l = 1.
Здесь p, q, l - конкретные числа (в том числе отрицательные). Этот вид уравнения удобен, когда необходимо изобразить в прямоугольной системе координат плоскость, поскольку числа p, q, l показывают точки пересечения с осями x, y и z плоскости.
Заметим, что каждый вид уравнения может быть преобразован в любой другой с помощью несложных математических операций.
Формула угла между двумя плоскостями
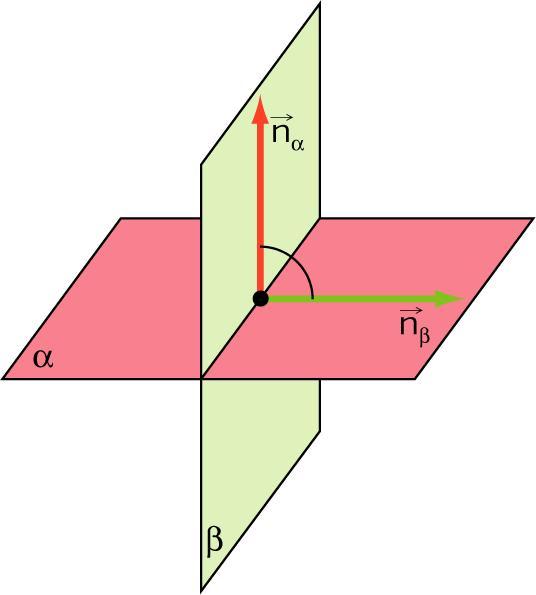
Теперь рассмотрим следующий нюанс. В трехмерном пространстве две плоскости могут располагаться всего двумя способами. Либо пересекаться, либо быть параллельными. Между двумя плоскостями углом называется то, что расположено между их векторами направляющими (нормальными). Пересекаясь, 2 вектора образуют 2 угла (острый и тупой в общем случае). В качестве угла между плоскостями принято считать острый. Рассмотрим уравнение.
Формула угла между двумя плоскостями имеет вид:
θ = arccos(|(n1¯*n2¯)|/(|n1¯|*|n2¯|)).
Несложно догадаться, что это выражение является прямым следствием из скалярного произведения нормальных векторов n1¯ и n2¯ для рассматриваемых плоскостей. Модуль скалярного произведения в числителе указывает на то, что угол θ будет принимать только значения от 0o до 90o. Произведение модулей нормальных векторов в знаменателе означает произведение их длин.
Отметим, если (n1¯*n2¯) = 0, то плоскости пересекаются под прямым углом.
Пример задачи
Разобравшись, что называется углом между двумя плоскостями, решим следующую задачу. В качестве примера. Итак, необходимо вычислить угол между такими плоскостями:
2*x - 3*y + 4 = 0;
(x, y, z) = (2, 0, -1) + α*(1, 1, -1) + β*(0, 2, 3).
Для решения задачи необходимо знать направляющие вектора плоскостей. Для первой плоскости нормальный вектор равен: n1¯ = (2, -3, 0). Чтобы найти второй плоскости нормальный вектор, следует умножить вектора, стоящие после параметров α и β. В результате получим вектор: n2¯ = (5, -3, 2).
Для определения угла θ воспользуемся формулой из предыдущего пункта. Получаем:
θ = arccos (|((2, -3, 0)*(5, -3, 2))|/(|(2, -3, 0)|*|(5, -3, 2)|)) =
= arccos (19/√(13*38)) = 0,5455 рад.
Рассчитанный угол в радианах соответствует 31,26o. Таким образом, плоскости из условия задачи пересекаются под углом 31,26o.
