Сеть убеждений, решений, байесовская (ian) модель или вероятностно-ориентированная ациклическая графическая модель - это вариативная схема (тип статистической модели), которая представляет набор переменных и их условных зависимостей через направленный ациклический график (DAG).
Например, байесовская сеть может представлять вероятностные отношения между заболеваниями и симптомами. Учитывая последние, сеть можно использовать для расчета возможности наличия различных заболеваний. На видео ниже вы можете увидеть примера байесовской сети доверия с расчетами.
 Вам будет интересно:Байесовские сети: определение, примеры и принципы работы
Вам будет интересно:Байесовские сети: определение, примеры и принципы работы
Эффективность
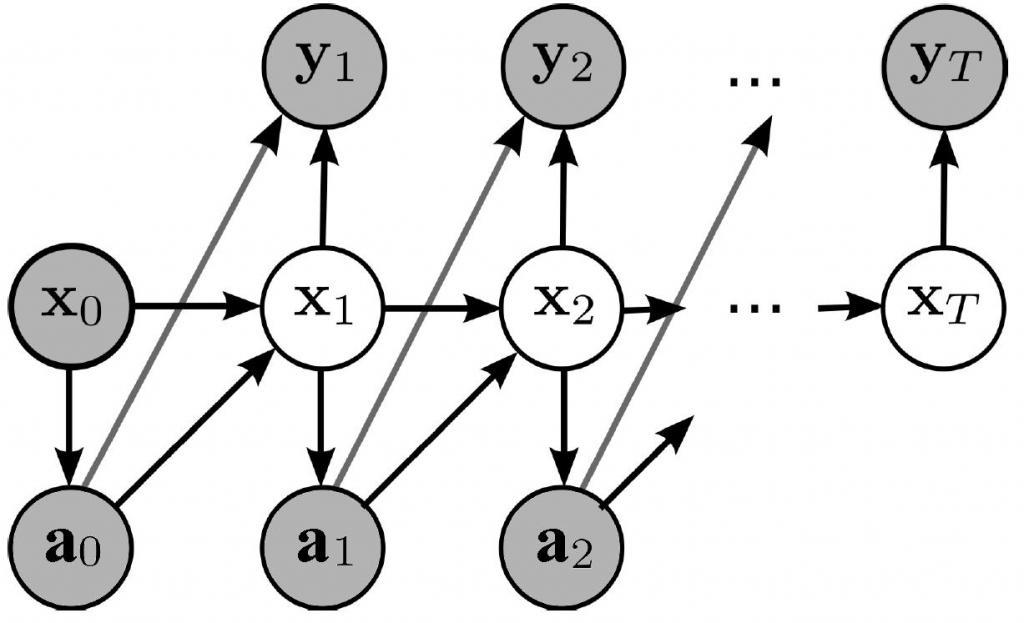
Эффективные алгоритмы могут выполнять вывод и обучение в байесовских сетях. Сети, которые моделируют переменные (например, речевые сигналы или белковые последовательности), называются динамическими. Обобщения байесовских сетей, которые могут представлять и решать задачи в условиях неопределенности, называются диаграммами влияния.
Суть
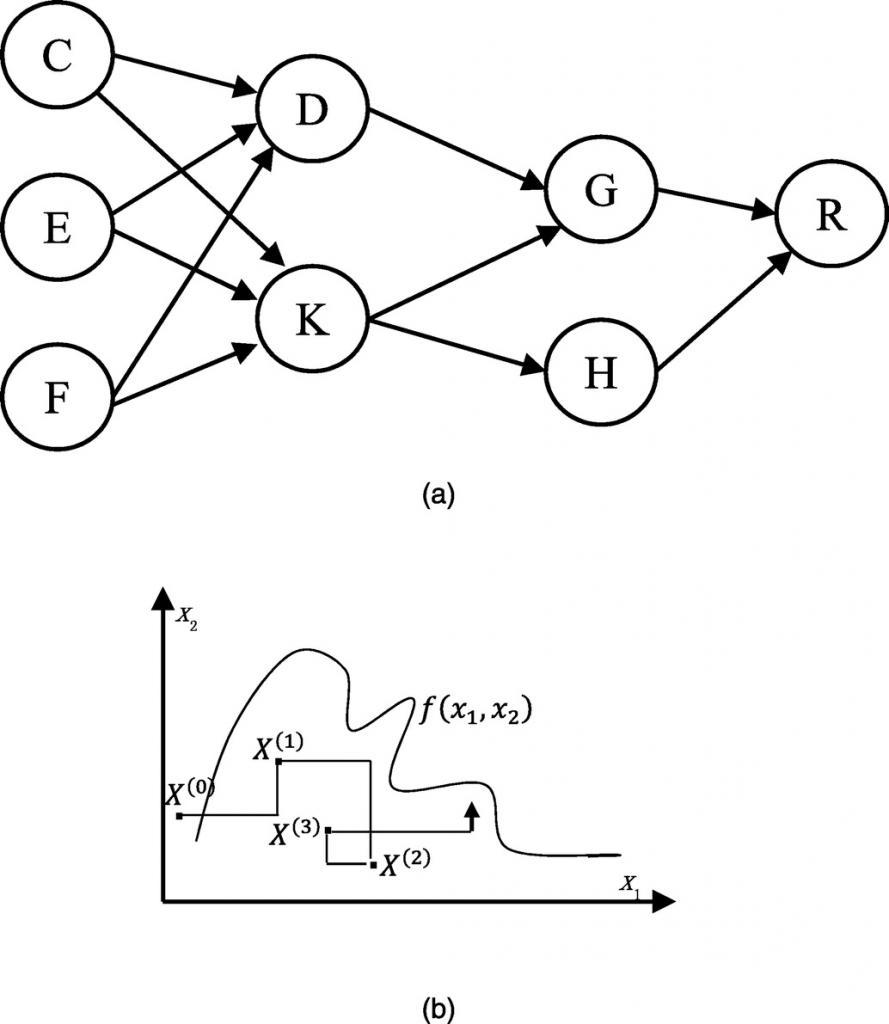
Формально байесовские сети - это группы доступности баз данных, узлы которых представляют переменные в байесовском смысле: это могут быть наблюдаемые величины, скрытые переменные, неизвестные параметры или гипотезы. Потому это очень интересно.
Пример байесовской сети
 Вам будет интересно:Вопрос на засыпку – это веселая игра или неловкая ситуация?
Вам будет интересно:Вопрос на засыпку – это веселая игра или неловкая ситуация?
Два события могут вызвать влажность травы: активный разбрызгиватель или дождь. Дождь оказывает непосредственное влияние на использование разбрызгивателя (а именно, что когда идет дождь, разбрызгиватель обычно не активен). Эта ситуация может быть смоделирована с помощью байесовской сети.
Моделирование
Поскольку байесовская сеть является полной моделью для ее переменных и их отношений, ее можно использовать для ответа на вероятностные запросы о них. Например, она может использоваться для обновления знаний о состоянии подмножества переменных, когда наблюдаются другие данные (переменные доказательства). Этот интересный процесс называется вероятностным выводом.
 Вам будет интересно:Признанная красавица Елена Михайловна Завадовская: биография, семья
Вам будет интересно:Признанная красавица Елена Михайловна Завадовская: биография, семья
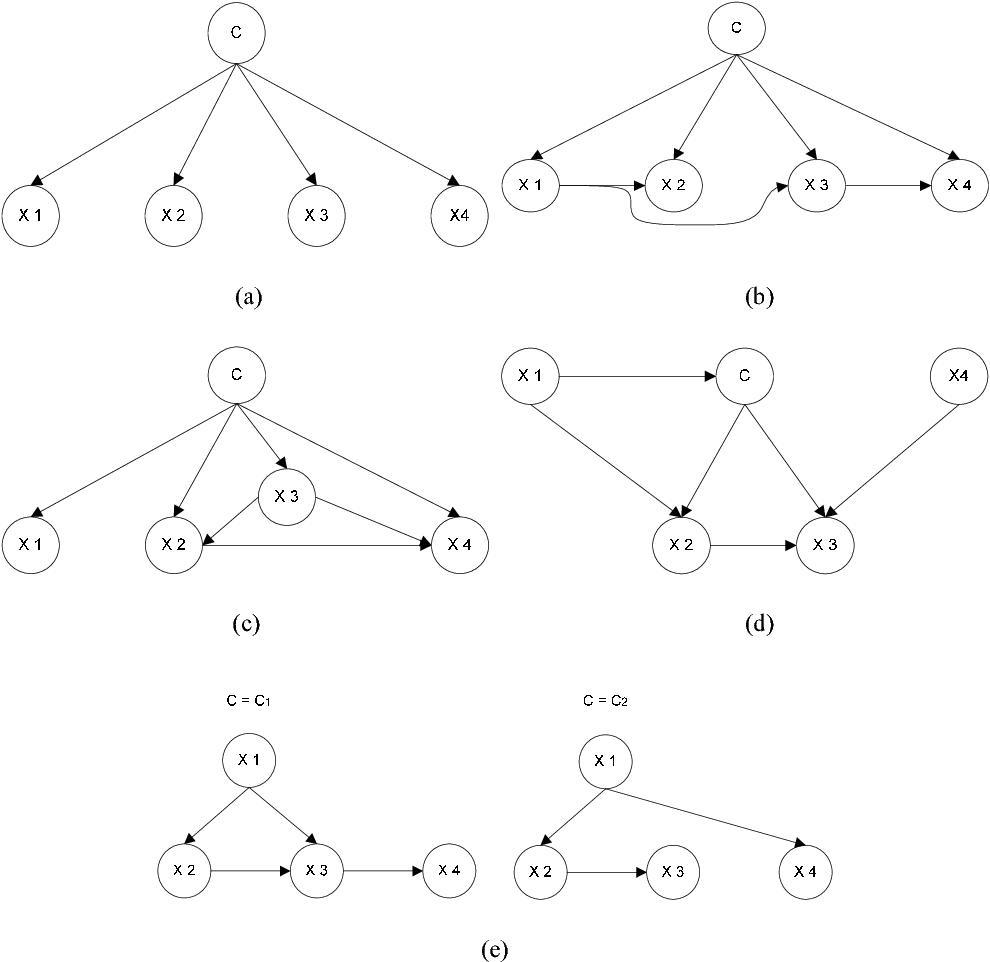
Апостериорный дает универсальную достаточную статистику для приложений обнаружения при выборе значений для подмножества переменных. Таким образом, данный алгоритм можно считать механизмом автоматического применения теоремы Байеса к сложным задачам. На картинках в статье вы можете увидеть примеры байесовских сетей доверия.
Методы вывода
Наиболее распространенными методами точного вывода являются: исключение переменных, которое устраняет (путем интегрирования или суммирования) не наблюдаемые параметры, не относящиеся к запросу, одну за другой путем распределения суммы по продукту.
Распространение "дерева" кликом, которое кэширует вычисления, так что многие переменные могут быть запрошены за один раз, и новые доказательства могут быть распространены быстро; и рекурсивное согласование и / или поиск, которые позволяют найти компромисс между пространством и временем и соответствуют эффективности исключения переменных, когда используется достаточно места.
Все эти методы имеют особую сложность, которая экспоненциально зависит от длины сети. Наиболее распространенными алгоритмами приближенного вывода являются такие способы, как устранение мини-сегментов, циклическое распространение убеждений, обобщенное распространение последних и вариационные методы.
Работа с сетями
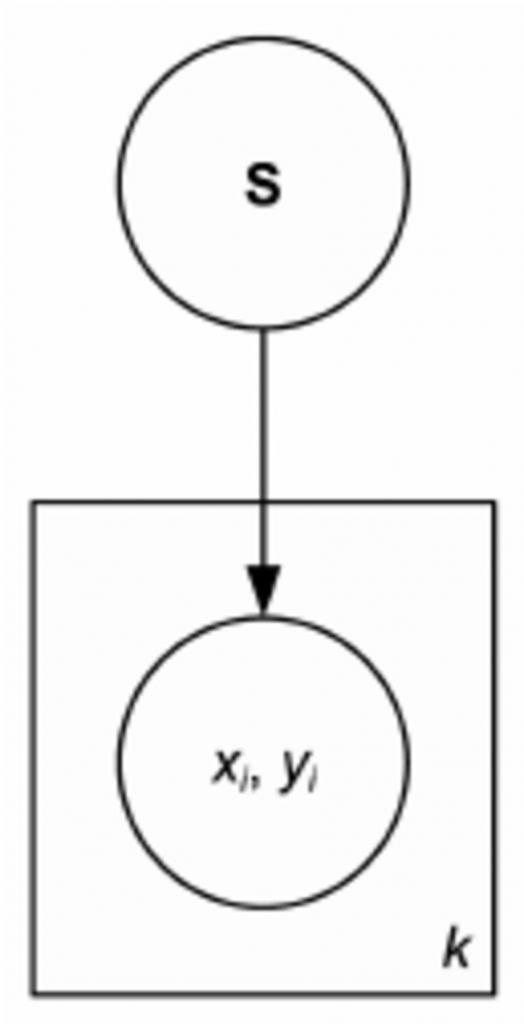
Чтобы полностью указать байесовскую сеть и, таким образом, полностью представить совместное распределение вероятностей, необходимо указать для каждого узла X распределение вероятностей для X, обусловленное родителями X.
Распределение X условно по его родителям может иметь любую форму. Распространено работать с дискретными или гауссовыми распределениями, поскольку это упрощает вычисления. Иногда известны только ограничения на распределение. Затем можно использовать энтропию для определения единственного распределения, которое имеет наибольшую энтропию с учетом ограничений.
Аналогично, в конкретном контексте динамической байесовской сети условное распределение для временной эволюции скрытого состояния обычно задается для максимизации скорости энтропии подразумеваемого случайного процесса.
Прямая максимизация вероятности (или апостериорной вероятности) часто бывает сложной, учитывая наличие ненаблюдаемых переменных. Это особенно характерно для байесовской сети принятия решений.
Классический подход
Классическим подходом к этой проблеме является алгоритм максимизации ожидания, который чередует вычисление ожидаемых значений ненаблюдаемых переменных, зависящих от наблюдаемых данных, с максимизацией полной вероятности (или апостериорного значения), предполагая, что ранее вычисленные ожидаемые значения верны. В условиях умеренной регулярности этот процесс сходится по максимальным (или максимальным апостериорным) значениям параметров.
Более полный байесовский подход к параметрам состоит в том, чтобы рассматривать их как дополнительные ненаблюдаемые переменные и вычислять полное апостериорное распределение по всем узлам с учетом наблюдаемых данных, а затем интегрировать параметры. Этот подход может быть дорогостоящим и приводить к моделям большого размера, делая классические подходы к настройке параметров более доступными.
В простейшем случае байесовская сеть определяется экспертом и затем используется для выполнения вывода. В других приложениях задача определения слишком сложна для человека. В этом случае структура байесовской нейронной сети и параметры локальных распределений должны быть изучены среди данных.
Альтернативный метод
Альтернативный метод структурного обучения использует оптимизационный поиск. Это требует применения функции оценки и стратегии поиска. Распространенным алгоритмом оценки является апостериорная вероятность структуры с учетом данных обучения, таких как BIC или BDeu.
Требуемое время для исчерпывающего поиска, возвращающего структуру, которая максимизирует оценку, является суперэкспоненциальным по числу переменных. Стратегия локального поиска вносит постепенные изменения, направленные на улучшение оценки структуры. Фридман и его коллеги рассматривали использование взаимной информации между переменными, чтобы найти нужную структуру. Они ограничивают набор родительских кандидатов k узлами и проводят тщательный поиск в них.
Особенно быстрый метод для точного изучения BN - представить проблему, как задачу оптимизации и решить ее с помощью целочисленного программирования. Ограничения ацикличности добавляются к целочисленной программе (IP) во время решения в виде плоскостей резания. Такой метод может обрабатывать проблемы с точностью до 100 переменных.
Решение проблем
Для решения проблем с тысячами переменных необходим другой подход. Один из них состоит в том, чтобы сначала выбрать один порядок, а затем найти оптимальную структуру BN относительно этого порядка. Это подразумевает работу в пространстве поиска возможного упорядочения, что удобно, так как оно меньше, чем пространство сетевых структур. Несколько заказов затем отбираются и оцениваются. Этот метод оказался наилучшим доступным в литературе, когда число переменных огромно.
Другой метод состоит в том, чтобы сосредоточиться на подклассе разложимых моделей, для которых MLE имеют замкнутую форму. Тогда можно обнаружить непротиворечивую структуру для сотен переменных.
Изучение байесовских сетей с ограниченной шириной трех линий необходимо для обеспечения точного, поддающегося трактовке вывода, поскольку сложность последнего в худшем случае является экспоненциальной по длине дерева k (согласно гипотезе экспоненциального времени). Тем не менее, как глобальное свойство графа, оно значительно увеличивает сложность процесса обучения. В этом контексте можно использовать K-дерево для эффективного обучения.
Развитие
Развитие байесовской сети доверия часто начинается с создания DAG G, такого, что X удовлетворяет локальному свойству Маркова относительно G. Иногда это причинный DAG. Оценены распределения условной вероятности каждой переменной по ее родителям в G. Во многих случаях, в частности, когда переменные являются дискретными, если совместное распределение X является произведением этих условных распределений, то X становится байесовской сетью относительно G.
Марковское "одеяло узла" - это множество узлов. Марковское одеяло делает узел независимым от остальной части в бланке одноименного узла и является достаточным знанием для расчета его распределения. X является байесовской сетью по отношению к G, если каждый узел условно независим от всех других узлов, учитывая его марковское одеяло.