Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.
Общие сведения о физической величине
Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.
Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:
 Вам будет интересно:Формулы момента силы для статики и динамики. Работа момента силы
Вам будет интересно:Формулы момента силы для статики и динамики. Работа момента силы
I = m * r².
Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).
Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:
I = ∫m(r² * dm) = ρ * ∫V(r² * dV).
Где ρ - плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.
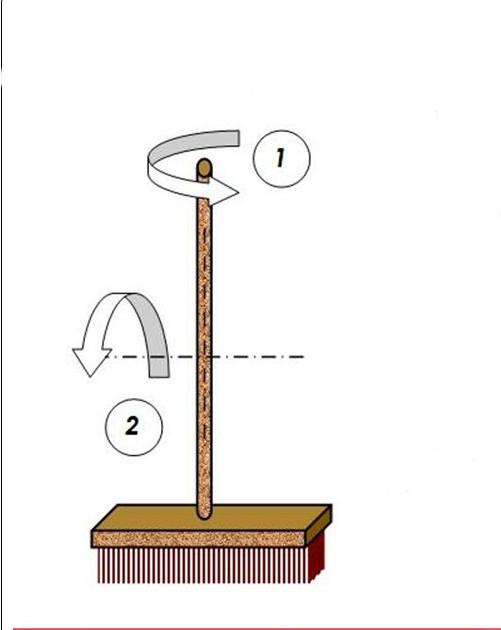
Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.
Величина I для тел разной формы
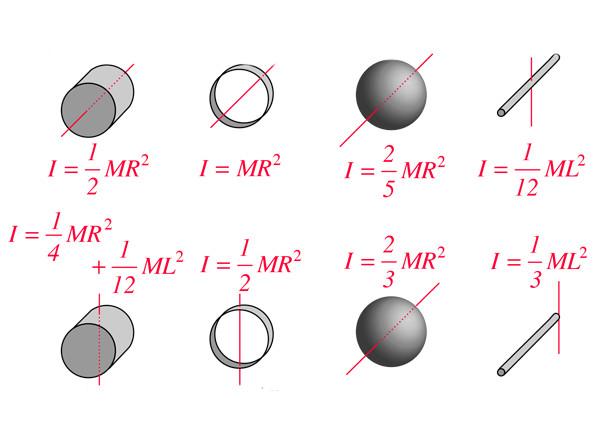
При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:
стержень: I = 1 / 12 * M * L²;
цилиндр: I = 1 / 2 * M * R²;
сфера: I = 2 / 5 * M * R².
Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.
Теорема Штейнера и формула
Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину IO тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром IO и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:
I = IO + M * h2.
Здесь M - масса тела, h - расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r0 + h.
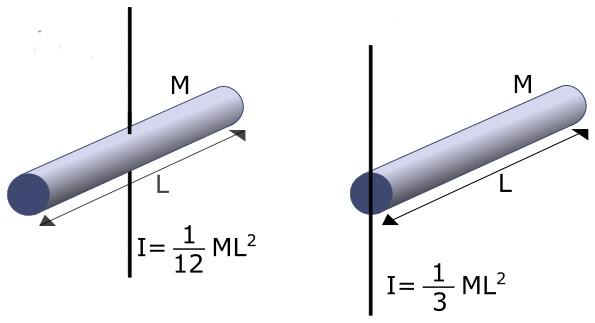
Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:
I = IO + M * (L / 2)2 = 1 / 12 * M * L2 + M * L2 / 4 = M * L2 / 3.
Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.
Уравнение моментов
В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:
M = I * α.
Здесь M - момент силы, α - угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:
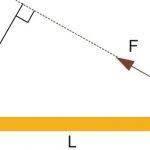
M = F * d.
Где d - плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.
Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.
Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.
Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:
I = IO + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².
Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:
M = F * d = 10 * 0,3 = 3 Н*м.
Теперь можно определить ускорение:
α = M/I = 3/0,09125 ≈ 32,9 рад/с².
Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.
