Одной из увлекательных и практически важных тем в физике является термодинамика газов. Системы, находящиеся в этом агрегатном состоянии, рассматривают с использованием так называемой модели идеального газа. Данная статья посвящена изучаемым в 10 классе изопроцессам в физике и решению задач на эту тему.
Модель идеального газа и уравнение состояния
Как известно, газы представляют собой высокоэнергетические системы, которые способны легко изменять свою форму и объем. Модель идеального газа заключается в том, что она предполагает отсутствие размеров у частиц и взаимодействия между ними. Справедливость этой модели очевидна в ряде практических случаев, поскольку расстояния между газовыми молекулами намного превышают их линейные размеры, а кинетическая энергия их движения на несколько порядков больше слабых взаимодействий между химически нейтральными частицами.
Вам будет интересно:Народная этимология: понятие, значение и применение в лингвистике
В 30-е годы XIX века, собирая и анализируя весь имеющийся экспериментальный материал, французский ученый Клапейрон записал универсальное уравнение, описывающее состояние любой идеальной газовой системы. Это уравнение имеет вид:
Вам будет интересно:Донкихотство - как это понимается в наши дни?
P*V = n*R*T.
Видно, что в равенстве содержатся все три основные термодинамические переменные (P - давление, V - объем и T - температура). Кроме того, оно не зависит от химических свойств системы, а определяется лишь количеством вещества n в ней. Символом R обозначена газовая постоянная, равная 8,314 Дж/(моль*К).
Изотермический процесс
Начнем изучать изопроцессы в физике с рассмотрения перехода системы между двумя равновесными состояниями при постоянной температуре. Если система является закрытой, то есть, она может обмениваться теплом с окружающей средой, но не с веществом, то правая часть равенства в приведенном выше уравнении состояния будет постоянной величиной. Этот факт приводит к следующему изотермическому закону:
P*V = const при T=const.
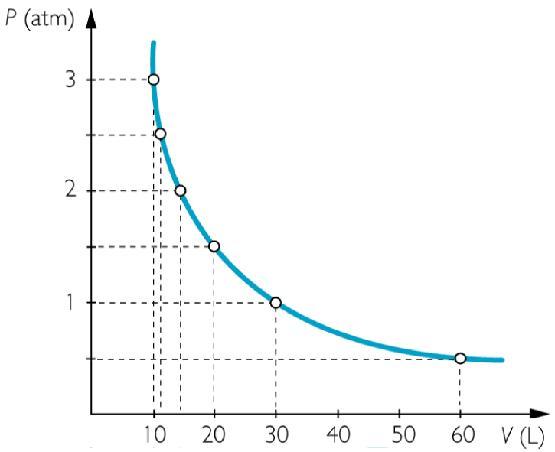
Это равенство называется законом Бойля-Мариотта в честь фамилий ученых, которые впервые обнаружили его экспериментально в XVII веке. Если изобразить изотерму в осях P и V, то она будет представлять собой гиперболу, показанную ниже на рисунке.
Пример задачи на закон Бойля-Мариотта
Решим следующую простую задачу по физике на изопроцессы (10 класс):
Известно, что газ под поршнем расширяется изотермически. Чему будет равно конечное давление в системе, если в начале оно составляло одну атмосферу? Объем в результате расширения газа увеличился в 3 раза.
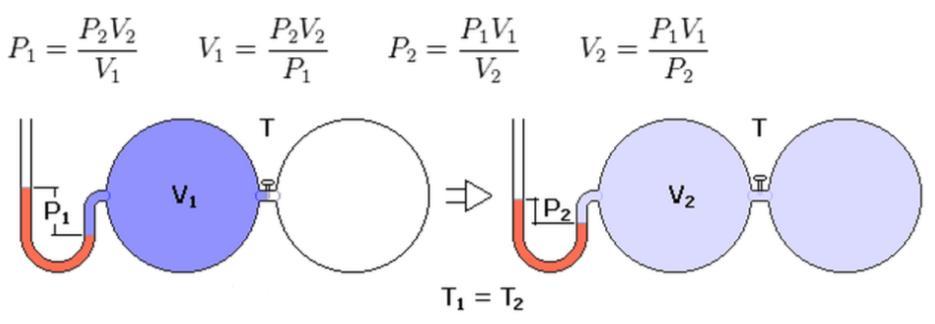
Запишем закон Бойля-Мариотта в таком виде:
P1*V1 = P2*V2.
Преобразуем это равенство таким образом, чтобы одинаковые физические величины оказались в одной части равенства:
P2/P1 = V1/V2.
Откуда получаем конечное выражение для P2 и ответ на вопрос задачи:
P2 = P1*V1/V2 = 1*1/3 = 0,33 атм.
Конечное давление в системе в 3 раза меньше начального.
Процессы изобарный и изохорный
Оба процесса специально были вынесены в один пункт статьи, поскольку они описываются математическими выражениями одной формы.
Если газовая система расширяется или сжимается, сохраняя постоянным давление, то говорят об изобарном процессе. В таком случае пользуются следующей формулой:
V/T = const при P = const.
Это выражение может быть получено из уравнения состояния. Оно называется законом Шарля (фамилия француза, открывшего закон в конце XVIII века).
Теперь предположим, что мы начали нагревать газ в твердом закрытом сосуде. Объем при этом будет оставаться постоянным. Что будет происходить с температурой и давлением в системе? Эксперименты и уравнение состояния говорят, что эти величины будут расти пропорционально друг другу, то есть:
P/T = const при V = const.
Описанный процесс называется изохорным, а закон, отражающий его, назван в честь француза Гей-Люссака, который первым его изучил экспериментально и опубликовал в начале XIX века.
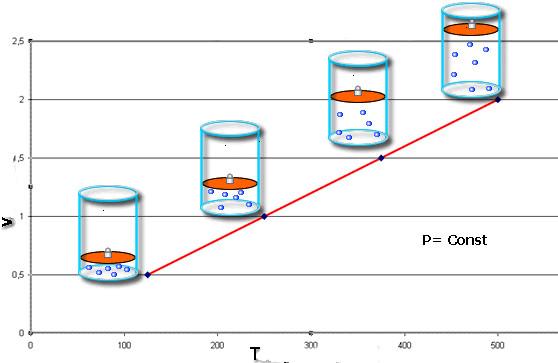
Из представленных формул следует, что их графическое изображение в осях V-T (изобара) и P-T (изохора) представляет собой прямолинейную зависимость. Пример изобары показан ниже.
Пример задачи на закон Шарля
Рассмотрим следующую задачу по физике на изопроцессы:
В одном цилиндре под подвижным поршнем содержится 2 моль некоторого газа при давлении 1 атмосфера. В другом цилиндре находится газ в количестве вещества 3 моль, давление в нем составляет 1,5 атмосферы. Оба цилиндра начали нагревать при постоянном давлении. Как будут взаимно расположены изобарные линии на графике в осях V-T для процессов в каждом цилиндре?
Чтобы ответить на поставленный вопрос, следует записать закон Шарля в таком виде:
V = const*T.
Это означает, что тангенс угла наклона для каждой прямой равен величине константы. Если ее найти для процессов в каждом цилиндре, то мы получим ответ на задачу. Для этого воспользуемся уравнением состояния, имеем:
P*V = n*R*T =>
V/T = n*R/P.
Правая часть последнего равенства является той самой константой, которую мы ищем. Как видно, она зависит прямо пропорционально от количества в системе вещества и обратно пропорционально от давления. Подставляя эти величины из условия, получим значения констант для каждого процесса:
const1 = n1*R/P1 = 2/1*R = 2*R;
const2 = n2*R/P2 = 3/1,5*R = 2*R.
Таким образом, значения констант для обоих процессов равны, что означает полное совпадение графиков изобар. Заметим, что при вычислении констант мы подставляли давление в атмосферах. Равенство const1 и const2 не изменится, если подставить давления в паскалях.
Пример задачи на закон Гей-Люссака
Как было показано, успешное решение задач по физике на изопроцессы требует знания не только самих процессов, но и умения использовать для них уравнение состояния. Приведем пример еще одной подобной задачи.
Кислород массой 20 грамм находится в закрытом сосуде объемом 2 литра. Охлаждение сосуда на 10 градусов Цельсия привело падению давления в сосуде на некоторую величину. Необходимо определить конечное равновесное давление в системе, если в начале оно было равно одной атмосфере.
В задаче речь идет об изохорном переходе газообразного кислорода. Получим рабочую формулу для него. Для этого выразим отношение давления к температуре из уравнения состояния:
P/T = n*R/V = m*R/(M*V).
Где количество вещества n записано как отношение массы газа m к его молярной массе M. Пользуясь этим выражением, определим разницу между конечным и начальным давлениями, получаем:
P2 - P1 = m*R/(M*V)*(T2 - T1).
Откуда приходим к конечному выражению, позволяющему ответить на поставленный в задаче вопрос:
P2 = P1 + m*R/(M*V)*ΔT, где ΔT = T2 - T1.
Подставлять все известные величины в формулу следует в единицах СИ. После подстановки и проведения вычислений, приходим к ответу: P2 = 75343,75 Па, что равно давлению в 0,74 атмосферы.
