Молекулярно-кинетическая теория позволяет, анализируя микроскопическое поведение системы и используя методы статистической механики, получить важные макроскопические характеристики термодинамической системы. Одной из микроскопических характеристик, которая связана с температурой системы, является средняя квадратичная скорость молекул газа. Формулу для нее приведем и рассмотрим в статье.
Газ идеальный
Сразу отметим, что формула квадратичной средней скорости молекул газа будет приведена именно для газа идеального. Под ним в физике полагают такую многочастичную систему, в которой частицы (атомы, молекулы) не взаимодействуют друг с другом (их кинетическая энергия на несколько порядков превышает потенциальную энергию взаимодействия) и не имеют размеров, то есть являются точками с конечной массой (расстояние между частицами на несколько порядков превышает их размеры линейные).
 Вам будет интересно:Порядок и правила приема в школу
Вам будет интересно:Порядок и правила приема в школу
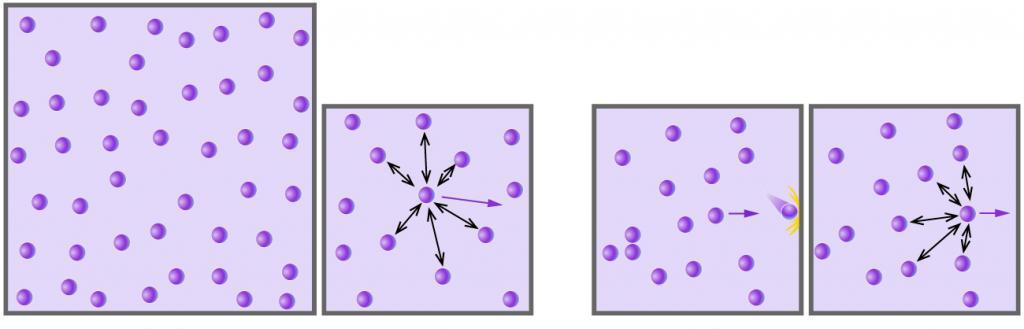
Любой газ, который состоит из химически нейтральных молекул или атомов, и что находится под небольшим давлением и имеет высокую температуру, может считаться идеальным. Например, воздух - это идеальный газ, а водяной пар таковым уже не является (между молекулами воды действуют сильные водородные связи).
Теория молекулярно-кинетическая (МКТ)

Изучая идеальный газ в рамках МКТ, следует обратить внимание на два важных процесса:
Несмотря на то, что индивидуальные скорости газовых частиц сильно отличаются друг от друга, среднее значение этой величины сохраняется постоянным во времени, если отсутствуют внешние воздействия на систему. Формулу средней квадратичной скорости молекул газа можно получить, если рассмотреть связь между кинетической энергией и температурой. Займемся этим вопросом в следующем пункте статьи.
Вывод формулы квадратичной средней скорости молекул газа идеального
Каждый школьник знает из общего курса физики, что кинетическая энергия поступательного движения тела массой m рассчитывается так:
Ek = m*v2/2
Где v - линейная скорость. С другой стороны, кинетическую энергию частицы также можно определить через абсолютную температуру T, используя переводной множитель kB (постоянная Больцмана). Поскольку наше пространство является трехмерным, то Ek рассчитывается так:
Ek = 3/2*kB*T.
Приравнивая оба равенства и выражая из них v, получим формулу средней скорости квадратичной газа идеального:
m*v2/2 = 3/2*kB*T =>
v = √(3*kB*T/m).
В этой формуле m - является массой газовой частицы. Ее значение неудобно использовать в практических расчетах, поскольку оно невелико (≈ 10-27 кг). Чтобы избежать этого неудобство вспомним об универсальной газовой постоянной R и молярной массе M. Постоянная R с kB связана равенством:
kB = R/NA.
Величина M определяется так:
M = m*NA.
Принимая во внимание оба равенства, получаем следующее выражение для средней квадратичной скорости молекул:
v = √(3*R*T/M).
Таким образом, средняя квадратичная скорость газовых частиц оказывается прямо пропорциональной квадратному корню из абсолютной температуры и обратно пропорциональна корню квадратному из молярной массы.
Пример решения задачи
Каждый знает, что воздух, которым мы дышим, на 99% состоит из азота и кислорода. Необходимо определить разницы в средних скоростях молекул N2 и O2 при температуре 15 oC.

Эту задачу будет решать последовательно. Сначала переведем температуру в абсолютные единицы, имеем:
T = 273,15 + 15 = 288,15 К.
Теперь выпишем молярные массы для каждой рассматриваемой молекулы:
MN2 = 0,028 кг/моль;
MO2 = 0,032 кг/моль.
Поскольку значения молярных масс отличаются между собой незначительно, то средние их скорости при одинаковой температуре тоже должны быть близки. Пользуясь формулой для v, получаем следующие значения для молекул азота и кислорода:
v (N2) = √(3*8,314*288,15/0,028) = 506,6 м/с;
v (O2) = √(3*8,314*288,15/0,032) = 473,9 м/с.
Поскольку молекулы азота немного легче, чем молекулы кислорода, то движутся они быстрее. Разница средних скоростей составляет:
v (N2) - v (O2) = 506,6 - 473,9 = 32,7 м/с.
Полученное значение составляет всего 6,5 % от средней скорости молекул азота. Обращаем внимание на большие значения скоростей молекул в газах даже при невысоких температурах.
