Раздел физики, который изучает покоящиеся тела с точки зрения механики, называется статикой. Ключевыми моментами статики являются понимание условий равновесия тел в системе и умение применять эти условия для решения практических задач.
Действующие силы
Причиной вращения, поступательного перемещения или сложного движения тел по кривым траекториям является действие внешней ненулевой силы на эти тела. В физике силой называется величина, которая, воздействуя на тело, способна придать ему ускорение, то есть изменить количество движения. Изучают эту величину с давних времен, тем не менее, законы статики и динамики окончательно оформились в стройную физическую теорию только с приходом нового времени. Большую роль в становлении механики движения сыграли работы Исаака Ньютона, в честь которого сейчас называют единицу измерения силы ньютоном.
Вам будет интересно:Древние расы: теории предыстории человечества, названия рас и причины гибели
При рассмотрении условий равновесия тел в физике важно знать несколько параметров действующих сил. К ним относятся следующие:
- направление действия;
- абсолютное значение;
- точка приложения;
- угол между рассматриваемой силой и другими приложенными к системе силами.
Вам будет интересно:«Ставок» — это про стоячую воду
Совокупность перечисленных параметров позволяет однозначно сказать, будет данная система двигаться или покоиться.
Первое условие равновесия системы
Когда система твердых тел не будет поступательно перемещаться в пространстве? Ответ на этот вопрос станет понятен, если вспомнить второй ньютоновский закон. Согласно ему, система не будет совершать поступательного перемещения тогда и только тогда, когда сумма внешних по отношению к системе сил равна нулю. То есть первое условие равновесия твердых тел математически выглядит так:
∑i=1nFi¯ = 0.
Здесь n - число внешних сил в системе. Приведенное выражение предполагает векторное суммирование сил.
Рассмотрим простой случай. Предположим, что на тело действуют две силы одинаковые по величине, но направленные в разные стороны. В итоге одна из них будет стремиться придать ускорение телу вдоль положительного направления произвольно выбранной оси, а другая - вдоль отрицательного. Результатом их действия будет покоящееся тело. Векторная сумма этих двух сил будет равна нулю. Справедливости ради отметим, что описанный пример приведет к появлению растягивающих напряжений в теле, но к теме статьи этот факт не относится.
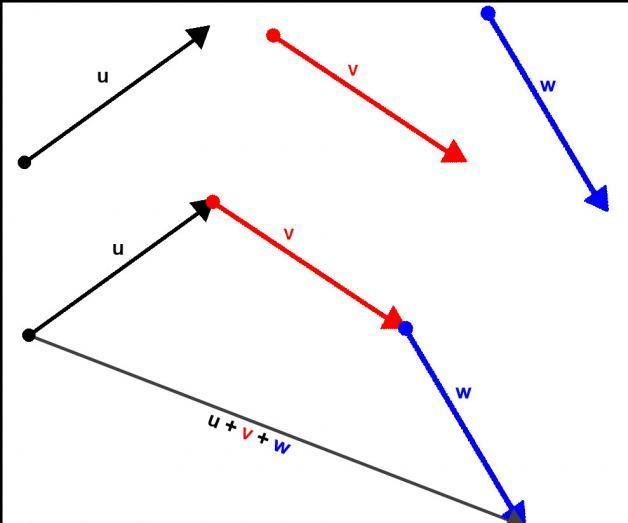
Для облегчения проверки записанного условия равновесия тел можно воспользоваться геометрическим изображением всех сил в системе. Если их векторы расположить так, чтобы каждая последующая сила начиналась из конца предыдущей, тогда записанное равенство будет выполняться, когда начало первой силы совпадет с концом последней. Геометрически это выглядит в виде замкнутого контура из векторов сил.
Момент силы
Прежде чем переходить к описанию следующего условия равновесия твердого тела, необходимо ввести важное физическое понятие статики - момент силы. Говоря простым языком, скалярная величина момента силы - это произведение модуля самой силы на радиус-вектор от оси вращения до точки приложения силы. Иными словами, момент силы имеет смысл рассматривать только относительно какой-либо оси вращения системы. Скалярная математическая форма записи момента силы выглядит так:
M = F*d.
Где d - плечо силы.
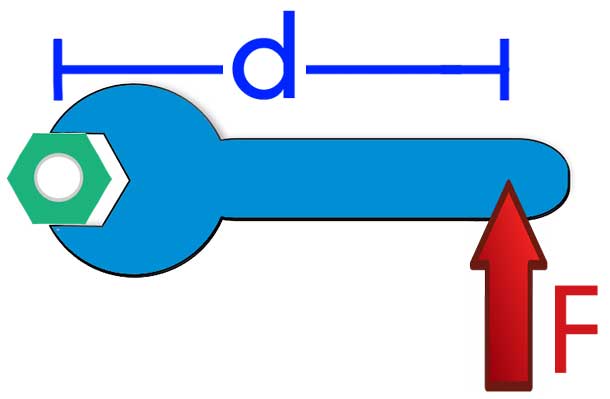
Из записанного выражения следует, что если сила F приложена к любой точке оси вращения под любым углом к ней, то ее момент силы будет равен нулю.
Физический смысл величины M заключается в способности силы F совершать поворот. Эта способность возрастает с увеличением расстояния между точкой приложения силы и осью вращения.
Второе условие равновесия системы
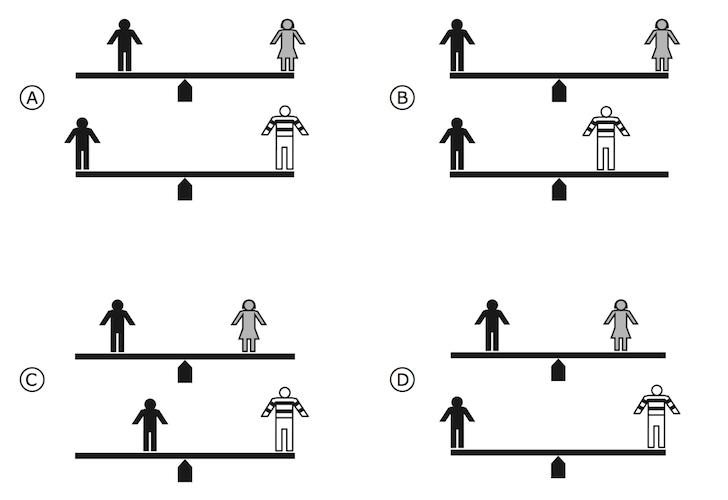
Как можно догадаться, второе условие равновесия тел с моментом силы связано. Сначала приведем соответствующую математическую формулу, а затем разберем ее подробнее. Итак, условие отсутствия вращения в системе записывается так:
∑i=1nMi = 0.
То есть сумма моментов всех сил должна быть равна нулю относительно каждой оси вращения в системе.
Момент силы является векторной величиной, однако для определения вращательного равновесия важно знать лишь знак данного момента Mi. Следует запомнить, что если сила стремится совершить вращение по ходу стрелки часов, значит, она создает отрицательный момент. Наоборот, вращение против хода стрелки приводит к появлению положительного момента Mi.
Методика определения равновесия системы
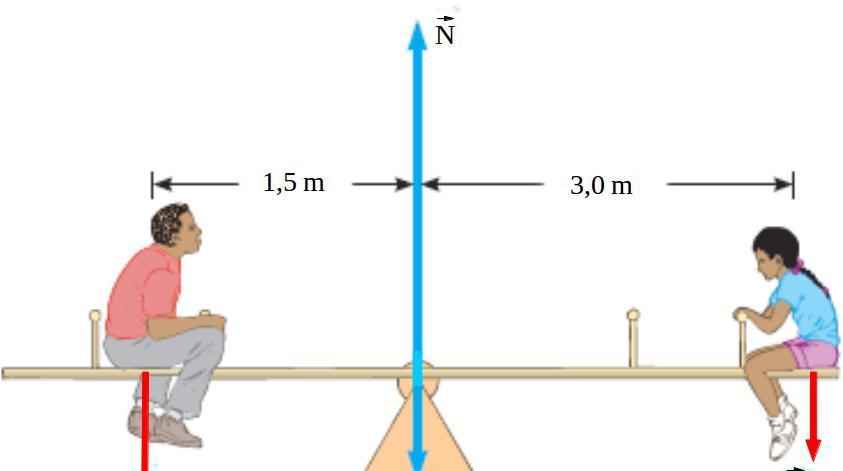
Выше были приведены два условия равновесия тел. Очевидно, что для того чтобы тело не двигалось и находилось в покое, необходимо одновременное выполнение обоих условий.
При решении задач на равновесие следует рассматривать систему из записанных двух уравнений. Решение этой системы даст ответ на любую задачу по статике.
Иногда первое условие, отражающее отсутствие поступательного движения, может не давать никакой полезной информации, тогда решение задачи сводится к анализу условия моментов.
При рассмотрении проблем статики на условия равновесия тел центр тяжести тела играет важную роль, поскольку именно через него проходит ось вращения. Если сумма моментов сил относительно центра тяжести будет равна нулю, тогда вращение системы наблюдаться не будет.
Пример решения задачи
Известно, что на концы невесомой доски положили два груза. Масса правого груза в два раза больше, чем масса левого. Необходимо определить положение опоры под доской, при которой данная система находилась бы в равновесии.
Обозначим длину доски буквой l, а расстояние от ее левого конца до опоры - буквой x. Ясно, что данная система не испытывает никакого поступательного движения, поэтому первое условие для решения задачи применять не нужно.
Вес каждого груза создает момент силы относительно опоры, причем оба момента имеют разный знак. В выбранных нами обозначениях, второе условие равновесия будет иметь вид:
P1*x = P2*(L-x).
Здесь P1 и P2 - веса левого и правого грузов, соответственно. Разделив на P1 обе части равенства, и используя условие задачи, получаем:
x = P2/P1*(L-x) =>
x = 2*L - 2*x =>
x = 2/3*L.
Таким образом, чтобы система находилась в равновесии, опора должна располагаться на 2/3 длины доски от левого ее конца (на 1/3 от правого конца).
