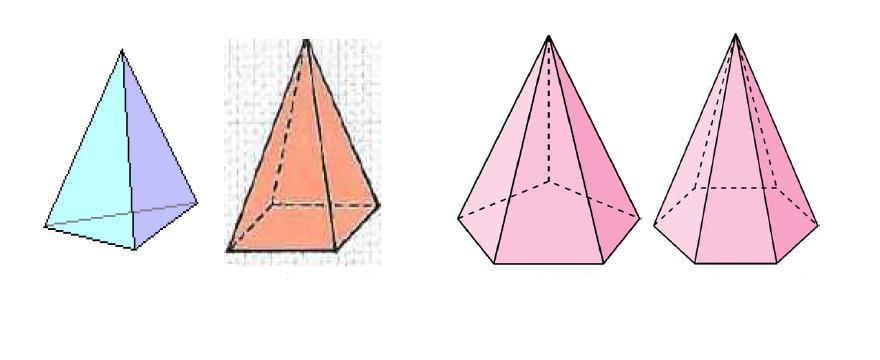
Типичными геометрическими задачами на плоскости и в трехмерном пространстве являются проблемы определения площадей поверхностей разных фигур. В данной статье приведем формулу площади боковой поверхности правильной пирамиды четырехугольной.
Что собой представляет пирамида?
Приведем строгое геометрическое определение пирамиды. Предположим, что имеется некоторый многоугольник с n сторонами и с n углами. Выберем произвольную точку пространства, которая не будет находиться в плоскости указанного n-угольника, и соединим ее с каждой вершиной многоугольника. Мы получим фигуру, имеющую некоторый объем, которая называется n-угольной пирамидой. Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.
 Вам будет интересно:Ставропольский региональный многопрофильный колледж: адрес, факультеты, условия поступления и педсостав
Вам будет интересно:Ставропольский региональный многопрофильный колледж: адрес, факультеты, условия поступления и педсостав

Два важных элемента любой пирамиды - это ее основание (n-угольник) и вершина. Эти элементы соединены друг с другом n треугольниками, которые в общем случае не равны друг другу. Перпендикуляр, опущенный из вершины к основанию, называется высотой фигуры. Если он пересекает основание в геометрическом центре (совпадает с центром масс многоугольника), то такую пирамиду называют прямой. Если помимо этого условия основание является правильным многоугольником, то и вся пирамида называется правильной. Рисунок ниже показывает, как выглядят правильные пирамиды с треугольным, четырехугольным, пятиугольным и шестиугольным основаниями.
Поверхность пирамиды
Прежде чем переходить к вопросу о площади боковой поверхности правильной пирамиды четырехугольной, следует подробнее остановиться на понятии самой поверхности.
Как было сказано выше и показано на рисунках, любая пирамида образована набором граней или сторон. Одна сторона является основанием, и n сторон представляют собой треугольники. Поверхность всей фигуры - это сумма площадей каждой ее стороны.
Поверхность удобно изучать на примере развертки фигуры. Развертка для правильной четырехугольной пирамиды приведена на рисунки ниже.
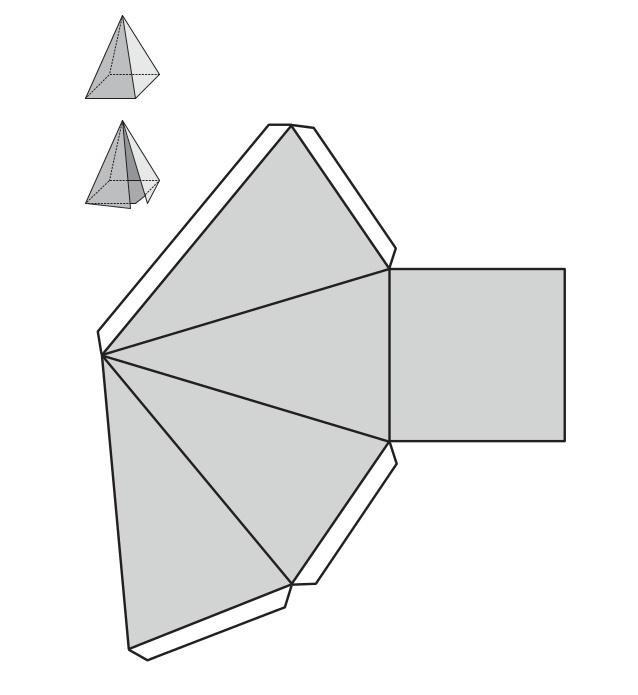
Видим, что площадь ее поверхности равна сумме четырех площадей одинаковых равнобедренных треугольников и площади квадрата.
Общую площадь всех треугольников, которые образуют боковые стороны фигуры, принято называть площадью боковой поверхности. Далее покажем, как ее рассчитать для четырехугольной пирамиды правильной.
Площадь боковой поверхности четырехугольной правильной пирамиды
Чтобы вычислить площадь боковой поверхности указанной фигуры, снова обратимся к приведенной выше развертке. Предположим, что нам известна сторона квадратного основания. Обозначим ее символом a. Видно, что каждый из четырех одинаковых треугольников, имеет основание длиной a. Чтобы вычислить их суммарную площадь, необходимо знать эту величину для одного треугольника. Из курса геометрии известно, что треугольника площадь St равна произведению основания на высоту, которое следует поделить пополам. То есть:
St = 1/2*hb*a.
Где hb - высота равнобедренного треугольника, проведенная к основанию a. Для пирамиды эта высота является апотемой. Теперь остается умножить полученное выражение на 4, чтобы получить площадь Sb поверхности боковой для рассматриваемой пирамиды:
Sb = 4*St = 2*hb*a.
Эта формула содержит два параметра: апотему и сторону основания. Если последняя в большинстве условий задач известна, то первую приходится вычислять, зная другие величины. Приведем формулы для расчета апотемы hb для двух случаев:
- когда известна длина бокового ребра;
- когда известна высота пирамиды.
Если обозначить длину ребра бокового (сторона равнобедренного треугольника) символом L, тогда апотема hb определиться по формуле:
hb = √(L2 - a2/4).
Это выражения является результатом применения теоремы Пифагора для треугольника боковой поверхности.
Если известна высота h пирамиды, тогда апотему hb можно рассчитать так:
hb = √(h2 + a2/4).
Получить это выражение также не сложно, если рассмотреть внутри пирамиды прямоугольный треугольник, образованный катетами h и a/2 и гипотенузой hb.
Покажем, как применять эти формулы, решив две интересные задачи.
Задача с известной площадью поверхности
Известно, что площадь боковой поверхности четырехугольной пирамиды правильной равна 108 см2. Необходимо вычислить значение длины ее апотемы hb, если высота пирамиды равна 7 см.
Запишем формулу площади Sb поверхности боковой через высоту. Имеем:
Sb = 2*√(h2 + a2/4) *a.
Здесь мы просто подставили соответствующую формулу апотемы в выражение для Sb. Возведем обе части равенства в квадрат:
Sb2 = 4*a2*h2 + a4.
Чтобы найти значение a, сделаем замену переменных:
a2 = t;
t2 + 4*h2*t - Sb2 = 0.
Подставляем теперь известные значения и решаем квадратное уравнение:
t2 + 196*t - 11664 = 0.
t ≈ 47,8355.
Мы выписали только положительный корень этого уравнения. Тогда стороны основания пирамиды будет равна:
a = √t = √47,8355 ≈ 6,916 см.
Чтобы получить длину апотемы, достаточно воспользоваться формулой:
hb = √(h2 + a2/4) = √(72 + 6,9162/4) ≈ 7,808 см.
Боковая поверхность пирамиды Хеопса

Определим значение площади поверхности боковой для самой большой египетской пирамиды. Известно, что в ее основании лежит квадрат с длиной стороны 230,363 метра. Высота сооружения изначально составляла 146,5 метра. Подставим эти цифры в соответствующую формулу для Sb, получим:
Sb = 2*√(h2 + a2/4) *a = 2*√(146,52+230,3632/4)*230,363 ≈ 85860 м2.
Найденное значение немного больше площади 17 футбольных полей.