Задачи с движущимися телами в физике, когда скорость много меньше световой, решаются с помощью законов ньютоновской, или классической механики. В ней одним из важных понятий является импульс. Основные формулы импульса в физике приводятся в данной статье.
Импульс или количество движения?
Прежде чем приводить формулы импульса тела в физике, познакомимся с этим понятием. Впервые величину под названием impeto (импульс) использовал в описании своих трудов Галилей в начале XVII века. Впоследствии Исаак Ньютон для нее употребил другое название - motus (движение). Поскольку фигура Ньютона оказала большее влияние на развитие классической физики, чем личность Галилея, изначально принято говорить не об импульсе тела, а о количестве движения.
Вам будет интересно:Ярославский политехнический университет (ЯГТУ): сведения, факты, поступление
Под количеством движения понимают произведение скорости перемещения тела на инерционный коэффициент, то есть на массу. Соответствующая формула имеет вид:
Вам будет интересно:Формулировка третьего закона Ньютона: примеры, связь с ускорением системы и с ее импульсом
p¯ = m*v¯
Здесь p¯ - вектор, направление которого совпадает с v¯, но модуль в m раз больше, чем модуль v¯.
Изменение величины p¯
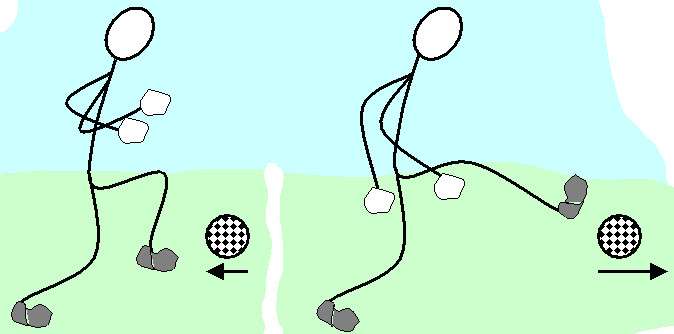
Понятие о количестве движения в настоящее время используют реже, чем об импульсе. И связан этот факт непосредственно с законами ньютоновской механики. Запишем его в форме, которая приводится в школьных учебниках по физике:
F¯ = m*a¯
Заменим ускорение a¯ на соответствующее выражение с производной скорости, получим:
F¯ = m*dv¯/dt
Перенося dt из знаменателя правой части равенства в числитель левой, получаем:
F¯*dt= m*dv¯ = dp¯
Мы получили интересный результат: помимо того, что действующая сила F¯ приводит к ускорению тела (см. первую формулу этого пункта), она также изменяет количество его движения. Произведение силы на время, которое стоит в левой части, называется импульсом силы. Он оказывается равным изменению величины p¯. Поэтому последнее выражение называют также формулой импульса в физике.
Заметим, что dp¯ - это тоже векторная величина, но направлена она в отличие от p¯ не как скорость v¯, а как сила F¯.
Ярким примером изменения вектора количества движения (импульса) является ситуация, когда футболист бьет по мячу. До удара мяч двигался к футболисту, после удара - от него.
Закон сохранения импульса
Формулы в физике, которые описывают сохранение величины p¯, могут быть приведены в нескольких вариантах. Прежде чем их записывать, ответим на вопрос о том, когда сохраняется импульс.
Обратимся к выражению из предыдущего пункта:
F¯*dt = dp¯
Оно говорит о том, что если сумма внешних сил, оказывающих воздействие на систему, равна нулю (закрытая система, F¯= 0), тогда dp¯= 0, то есть никакого изменения количества движения не будет происходить:
p¯ = const
Это выражение является общим для импульса тела и закона сохранения импульса в физике. Отметим два важных момента, о которых следует знать, чтобы с успехом применять это выражение на практике:
- Импульс сохраняется вдоль каждой координаты, то есть если до некоторого события значение px системы составляло 2 кг*м/c, то после этого события оно будет таким же.
- Импульс сохраняется независимо от характера столкновений твердых тел в системе. Известно два идеальных случая таких столкновений: абсолютно упругий и абсолютно пластичный удары. В первом случае сохраняется также кинетическая энергия, во втором часть ее расходуется на пластическую деформацию тел, однако импульс сохраняется все равно.
Упругое и неупругое взаимодействие двух тел
Частным случаем использования формулы импульса в физике и его сохранения является движение двух тел, которые сталкиваются друг с другом. Рассмотрим два принципиально разных случая, о которых упоминалось в пункте выше.
Если удар будет абсолютно упругим, то есть передача импульса от одного тела к другому осуществляется посредством упругой деформации, тогда формула сохранения p запишется так:
m1*v1 + m2*v2 = m1*u1 + m2*u2
Здесь важно помнить, что знак скорости должен подставляться с учетом ее направления вдоль рассматриваемой оси (противоположные скорости имеют разные знаки). Эта формула показывает, что при условии известного начального состояния системы (величины m1, v1, m2, v2) в конечном состоянии (после столкновения) имеется две неизвестных (u1, u2). Найти их можно, если воспользоваться соответствующим законом сохранения кинетической энергии:
m1*v12 + m2*v22 = m1*u12 + m2*u22
Если удар абсолютно неупругий или пластический, то после столкновения два тела начинают двигаться как единое целое. В этом случае имеет место выражение:
m1*v1 + m2*v2 = (m1 + m2)*u
Как видно, речь идет всего об одной неизвестной (u), поэтому для ее определения достаточно этого одного равенства.
Импульс тела во время движения по окружности
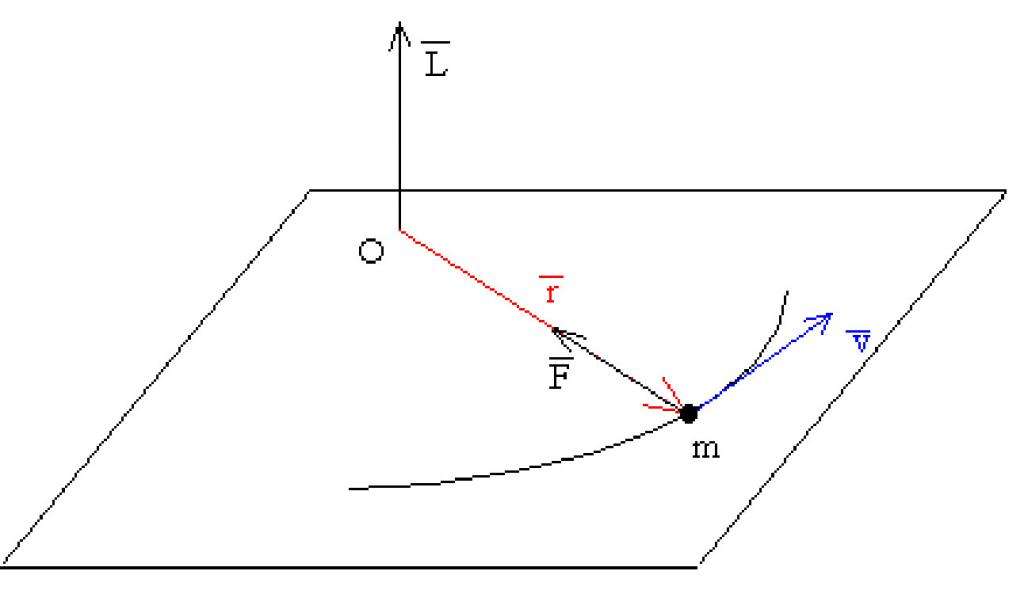
Все, что было сказано выше об импульсе, относится к линейным перемещениям тел. Как быть в случае вращения объектов вокруг оси? Для этого в физике введено другое понятие, которое аналогично линейному импульсу. Оно называется моментом импульса. Формула в физике для него принимает следующий вид:
L¯ = r¯*p¯
Здесь r¯ - вектор, равный расстоянию от оси вращения до частицы с импульсом p¯, совершающей круговые движения вокруг этой оси. Величина L¯ - это тоже вектор, но рассчитать его несколько сложнее, чем p¯, поскольку речь идет о векторном произведении.
Закон сохранения L¯
Формула для L¯, которая приведена выше, является определением этой величины. На практике же предпочитают использовать несколько иное выражение. Не будем вдаваться в подробности его получения (это несложно, и каждый может проделать это самостоятельно), а приведем его сразу:
L¯ = I*ω¯
Здесь I - это момент инерции (для материальной точки он равен m*r2), который описывает инерционные свойства вращающегося объекта, ω¯ - скорость угловая. Как можно заметить, это уравнение аналогично по форме записи такового для линейного импульса p¯.
Если на вращающую систему не действуют никакие внешние силы (в действительности момент сил), то произведение I на ω¯ будет сохраняться независимо от процессов, происходящих внутри системы. То есть закон сохранения для L¯ имеет вид:
I*ω¯ = const
Примером его проявления является выступление спортсменов в фигурном катании, когда они совершают вращения на льду.
