Любые задачи на движущиеся тела в классической механике требуют знания концепции импульса. В данной статье рассматривается эта концепция, дается ответ на вопрос, куда направлен вектор импульса тела, а также приводится пример решения задачи.
Количество движения

Чтобы выяснить, куда направлен вектор импульса тела, следует, в первую очередь, понять его физический смысл. Впервые термин был объяснен Исааком Ньютоном, однако важно отметить, что итальянский ученый Галилео Галилей в своих работах уже использовал похожее понятие. Для характеристики движущегося объекта он ввел величину, которая называлась стремление, натиск или собственно импульс (impeto на итальянском). Заслуга же Исаака Ньютона заключается в том, что он смог связать эту характеристику с действующими на тело силами.
 Вам будет интересно:Гипертекст - это в информатике что такое? Кем был введен термин "гипертекст"?
Вам будет интересно:Гипертекст - это в информатике что такое? Кем был введен термин "гипертекст"?
Итак, изначально и более правильно то, что большинство понимают под импульсом тела, называть количеством движения. Действительно, математическая формула для рассматриваемой величины пишется в виде:
 Вам будет интересно:Как это - "подытожить"? Что означает и как пишется?
Вам будет интересно:Как это - "подытожить"? Что означает и как пишется?
p¯ = m * v¯.
Здесь m - масса тела, v¯ - его скорость. Как видно из формулы, ни о каком импульсе речь не идет, имеется лишь скорость тела и его масса, то есть количество движения.
Важно отметить, что эта формула не следует из математических доказательств или выражений. Ее возникновение в физике имеет исключительно интуитивный, бытовой характер. Так, любой человек хорошо представляет, что если муха и грузовик будут двигаться с одинаковой скоростью, то грузовик остановить гораздо тяжелее, поскольку он обладает намного большим количеством движения, чем насекомое.

Откуда возникло понятие вектор импульса тела, рассмотрено далее.
Импульс силы - причина изменения количества движения
Интуитивно введенную характеристику Ньютон смог связать со вторым законом, носящим его фамилию.
 Вам будет интересно:Алифатическая аминокислота: что это?
Вам будет интересно:Алифатическая аминокислота: что это?
Импульс силы - это известная физическая величина, которая равна произведению приложенной внешней силы к некоторому телу на время ее действия. Воспользовавшись известным законом Ньютона и полагая, что сила от времени не зависит, можно прийти к выражению:
F¯ * Δt = m * a¯ * Δt.
Здесь Δt - время действия силы F, a - это линейное ускорение, сообщаемое силой F телу массой m. Как известно, умножение ускорения тела на промежуток времени, который оно действует, дает приращение скорости. Этот факт позволяет переписать формулу выше в несколько ином виде:
F¯ * Δt = m * Δv¯, где Δv¯= a¯ * Δt.
Правая часть равенства представляет собой изменение количества движения (см. выражение в предыдущем пункте). Тогда получится:
F¯ * Δt = Δp¯, где Δp¯ = m * Δv¯.
Таким образом, пользуясь законом Ньютона и понятием об импульсе силы, можно прийти к важному выводу: воздействие внешней силы на объект в течение некоторого времени приводит к изменению его количества движения.
Теперь становится понятным, почему количество движения принято называть импульсом, ведь его изменение совпадает с импульсом силы (слово "сила", как правило, опускают).
Векторная величина p¯
Над некоторыми величинами (F¯, v¯, a¯, p¯) стоит черта. Это означает, что речь идет о векторной характеристике. То есть количество движения так же, как и скорость, сила и ускорение, помимо абсолютной величины (модуля), описывается еще направлением.
Так как каждый вектор можно разложить на отдельные компоненты, то, пользуясь декартовой прямоугольной системой координат, можно записать следующие равенства:
1) p¯ = m * v¯;
2) px = m * vx; py = m * vy; pz = m * vz;
3) |p¯| = √(px2 + py2 + pz2).
Здесь 1-е выражение - это векторная форма представления количества движения, 2-й набор формул позволяет рассчитать каждую из компонентов импульса p¯, зная соответствующие компоненты скорости (индексы x, y, z говорят о проекции вектора на соответствующую ось координат). Наконец, 3-я формула позволяет вычислить длину вектора импульса (абсолютное значение величины) через его компоненты.
Куда направлен вектор импульса тела?
Рассмотрев понятие количества движения p¯ и его основные свойства, можно легко ответить на поставленный вопрос. Вектор импульса тела направлен так же, как и вектор линейной скорости. Действительно, из математики известно, что умножение вектора a¯ на число k приводит к образованию нового вектора b¯, обладающего следующими свойствами:
- его длина равна произведению числа на модуль исходного вектора, то есть |b¯| = k * |a¯|;
- он направлен так же, как исходный вектор, если k > 0, в противном случае он будет направлен противоположно a¯.
В данном случае роль вектора a¯ играет скорость v¯, импульс p¯ - это новый вектор b¯, а число k - это масса тела m. Поскольку последняя всегда является положительной (m>0), то, отвечая на вопрос: чему сонаправлен вектор импульса тела p¯, следует сказать, что он сонаправлен скорости v¯.
Вектор изменения количества движения
Интересно рассмотреть еще один похожий вопрос: куда направлен вектор изменения импульса тела, то есть Δp¯. Для ответа на него стоит использовать полученную выше формулу:
F¯ * Δt = m * Δv¯ = Δp¯.
Исходя из рассуждений в предыдущем пункте, можно сказать, что направление изменения количества движения Δp¯ совпадает с направлением вектора силы F¯ (Δt > 0) или с направлением вектора изменения скорости Δv¯ (m > 0).
Здесь важно не путать, что речь идет именно об изменении величин. В общем случае векторы p¯ и Δp¯ не совпадают, поскольку они никак не связаны друг с другом. Например, если сила F¯ будет действовать против скорости v¯ перемещения объекта, тогда p¯ и Δp¯ будут направлены в противоположные стороны.
Где важно учитывать векторный характер количества движения?

Рассмотренные выше вопросы: куда направлен вектор импульса тела и вектор его изменения, обусловлены не простым любопытством. Дело в том, что закон сохранения импульса p¯ выполняется для каждой его компоненты. То есть в наиболее полной форме он записывается так:
px = m * vx; py = m * vy; pz = m * vz.
Каждая компонента вектора p¯ сохраняет свое значение в системе взаимодействующих объектов, на которые не действуют внешние силы (Δp¯ = 0).
Как пользоваться этим законом и векторными представлениями величины p¯, чтобы решать задачи на взаимодействие (соударение) тел?
Задача с двумя шарами
На рисунке ниже изображены два шара разной массы, которые летят под разными углами к горизонтальной линии. Пусть массы шаров равны m1 = 1 кг, m2 = 0,5 кг, их скорости v1= 2 м/с, v2= 3 м/с. Необходимо определить направление импульса после удара шаров, полагая последний абсолютно неупругим.
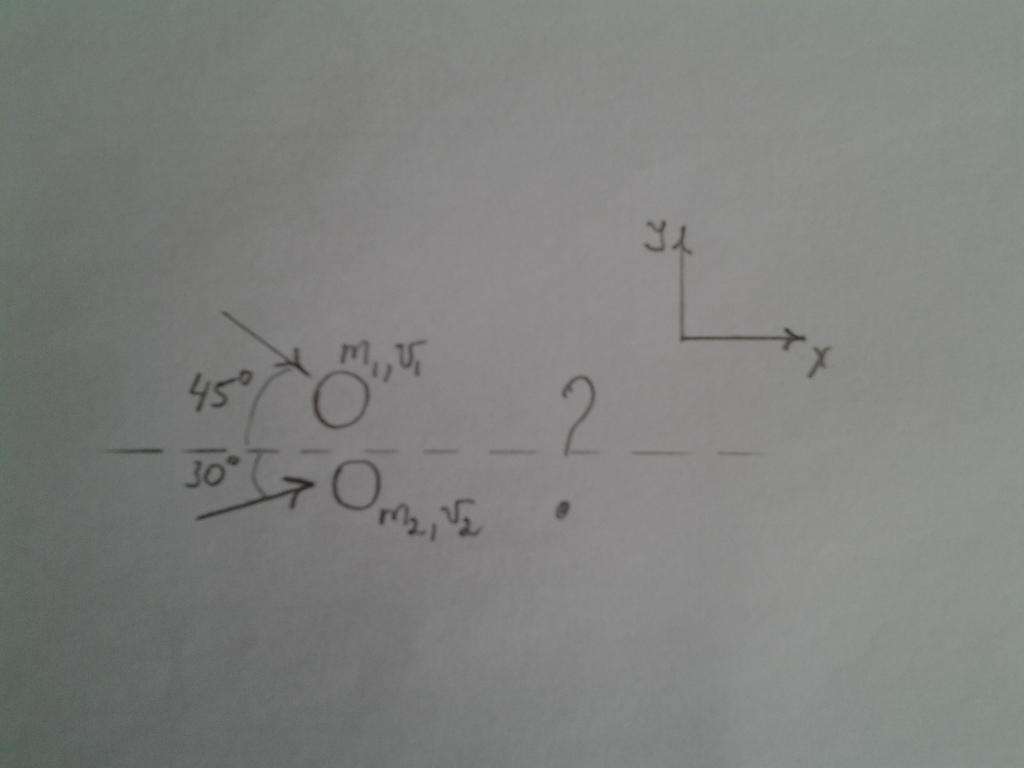
Начиная решать задачу, следует записать закон неизменности количества движения в векторной форме, то есть:
p1¯ + p2¯ = const.
Поскольку каждая компонента импульса должна сохраняться, то нужно переписать это выражение, учитывая также, что после столкновения два шара начнут двигаться, как единый объект (абсолютно неупругий удар):
m1 * v1x + m2 * v2x = (m1 + m2) * ux;
-m1 * v1y + m2 * v2y = (m1 + m2) * uy.
Знак минус для проекции импульса первого тела на ось y появился вследствие ее направленности против выбранного вектора оси ординат (см. рис.).
Теперь нужно выразить неизвестные компоненты скорости u, а затем подставить известные значения в выражения (соответствующие проекции скоростей определяются умножением модулей векторов v1¯ и v2¯ на тригонометрические функции):
ux = (m1 * v1x + m2 * v2x) / (m1 + m2), v1x = v1 * cos(45o); v2x = v2 * cos(30o);
ux = (1 * 2 * 0,7071 + 0,5 * 3 * 0,866) / (1 + 0,5) = 1,8088 м/с;
uy = (-m1 * v1y + m2 * v2y) / (m1 + m2), v1y = v1 * sin(45o); v2y = v2 * sin(30o);
uy = (-1 * 2 * 0,7071 + 0,5 * 3 * 0,5) / (1 + 0,5) = -0,4428 м/с.
Это две компоненты скорости тела после удара и "слипания" шаров. Поскольку направление скорости совпадает с вектором импульса p¯, то ответить на вопрос задачи можно, если определить u¯. Угол его относительно горизонтальной оси будет равен арктангенсу отношения компонент uy и ux:
α = arctg(-0,4428 / 1,8088) = -13,756o.
Знак минус указывает, что импульс (скорость) после удара будет направлен вниз от оси x.
