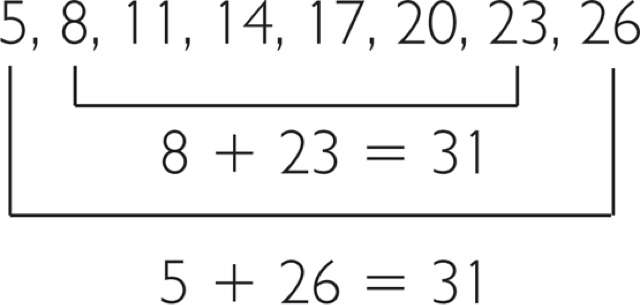- Что собой представляет арифметическая прогрессия
- Важные формулы
- Пример №1: нахождение неизвестного члена
- Пример №2: разность прогрессии
- Пример №3: составление прогрессии
- Пример №4: первый член прогрессии
- Пример №5: сумма
- Пример №6: сумма членов от n до m
- Некоторые советы при решении задач с арифметической прогрессией
При изучении алгебры в общеобразовательной школе (9 класс) одной из важных тем является изучение числовых последовательностей, к которым относятся прогрессии -геометрическая и арифметическая. В данной статье рассмотрим арифметическую прогрессию и примеры с решениями.
Что собой представляет арифметическая прогрессия?

Чтобы это понять, необходимо дать определение рассматриваемой прогрессии, а также привести основные формулы, которые далее будут использованы при решении задач.
 Вам будет интересно:Правописание: "непричем" или же "ни при чем"?
Вам будет интересно:Правописание: "непричем" или же "ни при чем"?
Арифметическая или алгебраическая прогрессия - это такой набор упорядоченных рациональных чисел, каждый член которого отличается от предыдущего на некоторую постоянную величину. Эта величина называется разностью. То есть, зная любой член упорядоченного ряда чисел и разность, можно восстановить всю арифметическую прогрессию.
Приведем пример. Следующая последовательность чисел будет прогрессией арифметической: 4, 8, 12, 16, ..., поскольку разность в этом случае равна 4 (8 - 4 = 12 - 8 = 16 - 12). А вот набор чисел 3, 5, 8, 12, 17 уже нельзя отнести к рассматриваемому виду прогрессии, поскольку разность для него не является постоянной величиной (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).
 Вам будет интересно:Паула Гитлер - младшая сестра Адольфа Гитлера: биография, личная жизнь
Вам будет интересно:Паула Гитлер - младшая сестра Адольфа Гитлера: биография, личная жизнь
Важные формулы
Приведем теперь основные формулы, которые понадобятся для решения задач с использованием арифметической прогрессии. Обозначим символом an n-й член последовательности, где n - целое число. Разность обозначим латинской буквой d. Тогда справедливы следующие выражения:
Чтобы понять любые примеры арифметической прогрессии с решением в 9 классе, достаточно запомнить эти две формулы, поскольку на их использовании строятся любые задачи рассматриваемого типа. Также следует не забывать, что разность прогрессии определяется по формуле: d = an - an-1.
 Вам будет интересно:Почему Латинская Америка называется Латинской: исторические факты и современные споры
Вам будет интересно:Почему Латинская Америка называется Латинской: исторические факты и современные споры
Далее, в статье приводятся различные примеры применения этих выражений.
Пример №1: нахождение неизвестного члена
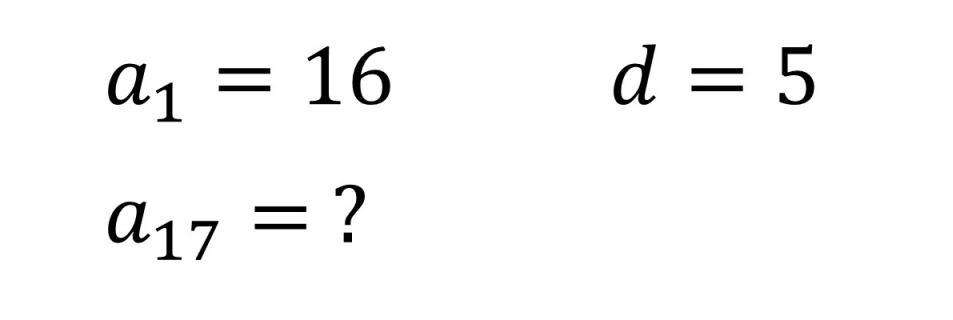
Приведем простой пример прогрессии арифметической и формул, которые необходимо использовать для решения.
Пусть дана последовательность 10, 8, 6, 4, ..., необходимо в ней найти пять членов.
Из условия задачи уже следует, что первые 4 слагаемых известны. Пятое можно определить двумя способами:
Как видно, оба способа решения привели к одному и тому же результату. Отметим, что в этом примере разность d прогрессии является отрицательной величиной. Такие последовательности называются убывающими, так как каждый следующий член меньше предыдущего.
Пример №2: разность прогрессии
Теперь усложним немного задачу, приведем пример, как найти разность прогрессии арифметической.
Известно, что в некоторой прогрессии алгебраической 1-й член равен 6, а 7-й член равен 18. Необходимо найти разность и восстановить эту последовательность до 7 члена.
Воспользуемся формулой для определения неизвестного члена: an = (n - 1) * d + a1. Подставим в нее известные данные из условия, то есть числа a1 и a7, имеем: 18 = 6 + 6 * d. Из этого выражения можно легко вычислить разность: d = (18 - 6) /6 = 2. Таким образом, ответили на первую часть задачи.
Чтобы восстановить последовательность до 7 члена, следует воспользоваться определением алгебраической прогрессии, то есть a2 = a1 + d, a3 = a2 + d и так далее. В итоге восстанавливаем всю последовательность: a1 = 6, a2 = 6 + 2=8, a3 = 8 + 2 = 10, a4 = 10 + 2 = 12, a5 = 12 + 2 = 14, a6 = 14 + 2 = 16, a7 = 18.
Пример №3: составление прогрессии
 Вам будет интересно:Признаки подобия и равенства треугольников. Свойства подобных треугольников
Вам будет интересно:Признаки подобия и равенства треугольников. Свойства подобных треугольников
Усложним еще сильнее условие задачи. Теперь необходимо ответить на вопрос, как находить арифметическую прогрессию. Можно привести следующий пример: даны два числа, например, - 4 и 5. Необходимо составить прогрессию алгебраическую так, чтобы между этими помещалось еще три члена.
Прежде чем начинать решать эту задачу, необходимо понять, какое место будут занимать заданные числа в будущей прогрессии. Поскольку между ними будут находиться еще три члена, тогда a1 = -4 и a5 = 5. Установив это, переходим к задаче, которая аналогична предыдущей. Снова для n-го члена воспользуемся формулой, получим: a5 = a1 + 4 * d. Откуда: d = (a5 - a1)/4 = (5 - (-4)) / 4 = 2,25. Здесь получили не целое значение разности, однако оно является рациональным числом, поэтому формулы для алгебраической прогрессии остаются теми же самыми.
Теперь добавим найденную разность к a1 и восстановим недостающие члены прогрессии. Получаем: a1 = - 4, a2 = - 4 + 2,25 = - 1,75, a3 = -1,75 + 2,25 = 0,5, a4 = 0,5 + 2,25 = 2,75, a5 = 2,75 + 2,25 = 5, что совпало с условием задачи.
Пример №4: первый член прогрессии

Продолжим приводить примеры арифметической прогрессии с решением. Во всех предыдущих задачах было известно первое число алгебраической прогрессии. Теперь рассмотрим задачу иного типа: пусть даны два числа, где a15 = 50 и a43 = 37. Необходимо найти, с какого числа начинается эта последовательность.
Формулы, которыми пользовались до настоящего времени, предполагают знание a1 и d. В условии задачи об этих числах ничего неизвестно. Тем не менее выпишем выражения для каждого члена, о котором имеется информация: a15 = a1 + 14 * d и a43 = a1 + 42 * d. Получили два уравнения, в которых 2 неизвестные величины (a1 и d). Это означает, что задача сводится к решению системы линейных уравнений.
Указанную систему проще всего решить, если выразить в каждом уравнении a1, а затем сравнить полученные выражения. Первое уравнение: a1 = a15 - 14 * d = 50 - 14 * d; второе уравнение: a1 = a43 - 42 * d = 37 - 42 * d. Приравнивая эти выражения, получим: 50 - 14 * d = 37 - 42 * d, откуда разность d = (37 - 50) / (42 - 14) = - 0,464 (приведены лишь 3 знака точности после запятой).
Зная d, можно воспользоваться любым из 2 приведенных выше выражений для a1. Например, первым: a1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496.
Если возникают сомнения в полученном результате, можно его проверить, например, определить 43 член прогрессии, который задан в условии. Получим: a43 = a1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Небольшая погрешность связана с тем, что при вычислениях использовалось округление до тысячных долей.
Пример №5: сумма
Теперь рассмотрим несколько примеров с решениями на сумму арифметической прогрессии.
Пусть дана числовая прогрессия следующего вида: 1, 2, 3, 4, ...,. Как рассчитать сумму 100 этих чисел?
Благодаря развитию компьютерных технологий можно эту задачку решить, то есть последовательно сложить все числа, что вычислительная машина сделает сразу же, как только человек нажмет клавишу Enter. Однако задачу можно решить в уме, если обратить внимание, что представленный ряд чисел является прогрессией алгебраической, причем ее разность равна 1. Применяя формулу для суммы, получаем: Sn = n * (a1 + an) / 2 = 100 * (1 + 100) / 2 = 5050.
Любопытно отметить, что эта задача носит название "гауссовой", поскольку в начале XVIII века знаменитый немецкий математик Гаусс, еще будучи в возрасте всего 10 лет, смог решить ее в уме за несколько секунд. Мальчик не знал формулы для суммы алгебраической прогрессии, но он заметил, что если складывать попарно числа, находящиеся на краях последовательности, то получается всегда один результат, то есть 1 + 100 = 2 + 99 = 3 + 98 = ..., а поскольку этих сумм будет ровно 50 (100 / 2), то для получения правильного ответа достаточно умножить 50 на 101.
Пример №6: сумма членов от n до m
Еще одним типичным примером суммы арифметической прогрессии является следующий: дан такой чисел ряд: 3, 7, 11, 15, ..., нужно найти, чему будет равна сумма его членов с 8 по 14.
Задача решается двумя способами. Первый из них предполагает нахождение неизвестных членов с 8 по 14, а затем их последовательное суммирование. Поскольку слагаемых немного, то такой способ не является достаточно трудоемким. Тем не менее предлагается решить эту задачу вторым методом, который является более универсальным.
Идея заключается в получении формулы для суммы алгебраической прогрессии между членами m и n, где n > m - целые числа. Выпишем для обоих случаев два выражения для суммы:
Поскольку n > m, то очевидно, что 2 сумма включает в себя первую. Последнее умозаключение означает, что если взять разность между этими суммами, и добавить к ней член am (в случае взятия разности он вычитается из суммы Sn), то получим необходимый ответ на задачу. Имеем: Smn = Sn - Sm + am =n * (a1 + an) / 2 - m *(a1 + am)/2 + am = a1 * (n - m) / 2 + an * n / 2 + am * (1- m/2). В это выражение необходимо подставить формулы для an и am. Тогда получим: Smn = a1 * (n - m) / 2 + n * (a1 + (n - 1) * d) / 2 + (a1 + (m - 1) * d) * (1 - m / 2) = a1 * (n - m + 1) + d * n * (n - 1) / 2 + d *(3 * m - m2 - 2) / 2.
Полученная формула является несколько громоздкой, тем не менее сумма Smn зависит только от n, m, a1 и d. В нашем случае a1 = 3, d = 4, n = 14, m = 8. Подставляя эти числа, получим: Smn = 301.
Некоторые советы при решении задач с арифметической прогрессией

Как видно из приведенных решений, все задачи основываются на знании выражения для n-го члена и формулы для суммы набора первых слагаемых. Перед тем как приступить к решению любой из этих задач, рекомендуется внимательно прочитать условие, ясно понять, что требуется найти, и лишь затем приступать к решению.
Еще один совет заключается в стремлении к простоте, то есть если можно ответить на вопрос, не применяя сложные математические выкладки, то необходимо поступать именно так, поскольку в этом случае вероятность допустить ошибку меньше. Например, в примере арифметической прогрессии с решением №6 можно было бы остановиться на формуле Smn = n * (a1 + an) / 2 - m * (a1 + am) / 2 + am, и разбить общую задачу на отдельные подзадачи (в данном случае сначала найти члены an и am).
Если возникают сомнения в полученном результате, то рекомендуется его проверять, как это было сделано в некоторых приведенных примерах. Как находить арифметическую прогрессию, выяснили. Если разобраться, то это не так сложно.