При рассмотрении перемещений тел и их систем в пространстве часто приходится рассчитывать работу тех или иных сил. В данной статье дадим определение механической работы в физике, объясним, как она связана с энергией, а также приведем примеры решения задач на эту тему.
В чем различие между энергией и работой?
При изучении работы в физике (9 класс общеобразовательных школ) многие ученики путают данную величину с энергией. Понять это можно: ведь обе характеристики определяются в джоулях. Тем не менее, энергия - это фундаментальная характеристика. Она не может появляться или исчезать, а способна лишь переходить в разные состояния и формы. В этом заключается суть закона ее сохранения в изолированной системе. Работа же - это одна из форм реализации энергии, которая приводит к пространственному перемещению тел.
 Вам будет интересно:Корпоративизм - это... Описание, особенности и цели
Вам будет интересно:Корпоративизм - это... Описание, особенности и цели
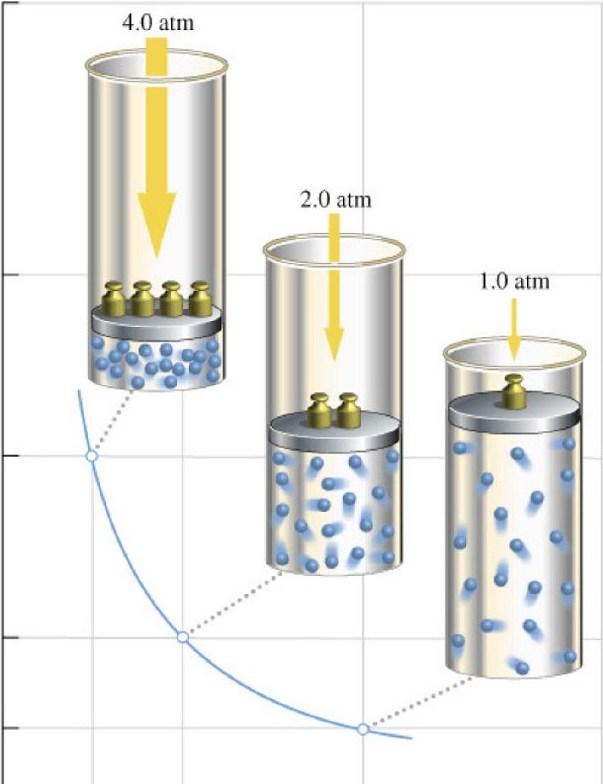
Так, при нагреве газа увеличивается его внутренняя энергия, то есть система получает возможность за счет нее совершить некоторую механическую работу. Последняя возникнет, когда газ начнет расширяться, увеличивать свой объем.
Строгое определение работы в физике
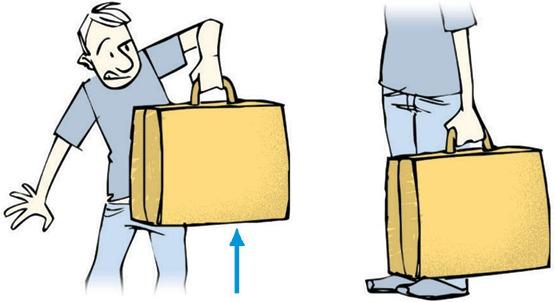
Строгим определением в физике является такое, которое предполагает четкое математическое обоснование. Применительно к рассматриваемой величине можно сказать следующее: если на тело действует некоторая сила F¯, в результате которой оно начинает перемещаться на вектор S¯, то работой A называется такая величина:
A = (F¯*S¯)
Поскольку A - это величина скалярная, то круглые скобки в правой части равенства говорят о том, что оба вектора умножаются скалярно.
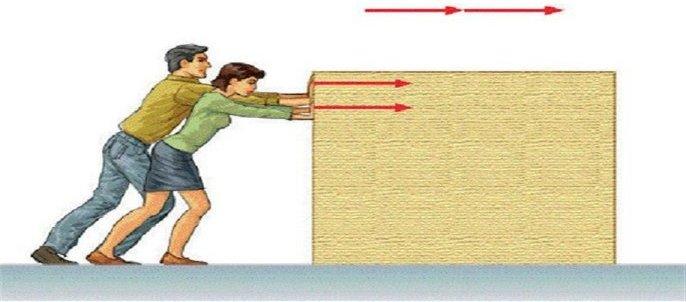
Из записанного выражения следует важный факт: если сила действует перпендикулярно перемещению, то работы она не совершает. Так, многие школьники при решении по физике контрольных работ в 10 классе, например, допускают частую ошибку. Они полагают, что перемещать горизонтально тяжелый груз трудно именно из-за силы тяжести. Как показывает формула работы, сила тяжести при горизонтальном перемещении совершает нулевую работу, поскольку она направлена вертикально вниз. В действительности, трудность перемещения тяжелого груза связана с действием силы трения, которая прямо пропорциональна силе тяготения.
Выражение для A в явном виде может быть записано так:
A = F*cos(φ)*S
Произведение F*cos(φ) представляет собой проекцию вектора силы на вектор перемещения.
Работа и КПД
Каждому известно, что создать механизм, который бы всю затраченную энергию переводил в полезную работу, оказывается невозможным на практике. В связи с этим ввели понятие коэффициента полезного действия (КПД). Рассчитать его несложно, если воспользоваться следующим выражением:
КПД = Ап/Аз*100 %
Здесь Ап, Аз - полезная и затраченная работы соответственно. При этом Аз всегда больше, чем Ап, поэтому КПД всегда меньше 100 %. Например, двигатель внутреннего сгорания имеет КПД в пределах 25-40 %. Эти цифры говорят о том, что большая часть топлива при сгорании расходуется на нагрев окружающей среды, а не на движение автомобиля.
В абсолютном большинстве случаев невозможность получить КПД = 100 % связано с постоянным присутствием сил трения. Даже в таком простом механизме, как рычаг, эти силы, действующие в области опоры, приводят к снижению КПД до 80-90 %.

Далее в статье решим пару задач по рассмотренной теме.
Задача с телом на наклонной плоскости
Тело массой 4 кг движется вертикально вверх по наклонной плоскости. Угол ее наклона относительно горизонта составляет 20o. На тело действует внешняя сила, которая равна 80 Н (она направлена горизонтально), а также сила трения, которая составляет 10 Н. Необходимо вычислить работу каждой из сил и общую работу, если тело двигалось вдоль плоскости 10 метров.
Прежде чем начать решать задачу, напомним, что, кроме указанных сил, на тело еще действует сила тяжести и реакции опоры. Последнюю можно не рассматривать, поскольку ее работа будет равна нулю. Сила же тяжести выполняет отрицательную работу, поскольку тело движется вверх по наклонной.
Сначала вычислим работу внешней силы F0. Она составит:
A0 = F0*S*cos(20o) = 751,75 Дж.
Заметим, что рассчитанная работа будет положительной, поскольку вектор внешней силы имеет острый угол с направлением перемещения.
Работы сил тяжести Fg и трения Ff будут отрицательными. Рассчитаем их с учетом угла наклона плоскости и направления перемещения тела:
A1 = -Fg*S*sin(20o) = -m*g*S*sin(20o) = -134,21 Дж;
A2 = -Ff*S = -10*10 = -100 Дж.
Общая работа всех сил будет равна сумме рассчитанных величин, то есть:
A = A0 + A1 + A2 = 751,75 - 134,21 - 100 = 517,54 Дж.
Эта работа тратится на увеличение кинетической энергии тела.
Задача со сложной зависимостью силы
Известно, что материальная точка движется вдоль прямой, изменяя свои координаты от x = 2 до x = 5 м. В процессе движения на нее оказывает действие сила F, которая изменяется по следующему закону:
F = 3*x2 + 2*x - 5 Н.
Полагая, что F действует вдоль линии перемещения точки, необходимо вычислить работу, которую она совершает.
Поскольку сила постоянно изменяется, то в лоб не получится использовать записанную в статье формулу для A. Чтобы рассчитать эту величину поступим следующим образом: вычислим на каждом элементарном отрезке пути dx работу dA, а затем, сложим все результаты. Рассуждая так, мы приходим к интегральной формуле для работы в физике:
A = ∫x(F*dx).
Теперь осталось вычислить этот интеграл для нашего случая:
A = ∫52((3*x2 + 2*x - 5)*dx) = (x3 + x2 - 5*x)|52 = 123 Дж.
Мы получили результат в джоулях, поскольку координата x выражается в метрах, а сила F в ньютонах.
