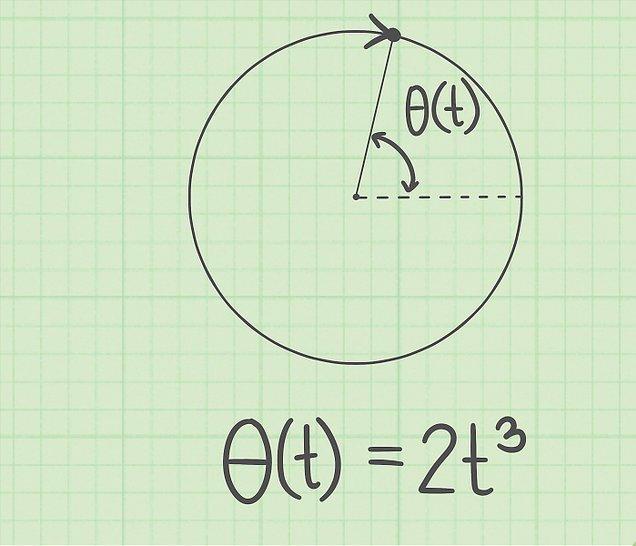В физике рассмотрением особенностей движения макроскопических твердых тел занимается кинематика. Этот раздел механики оперирует такими понятиями, как скорость, ускорение и путь. В данной статье мы сосредоточим свое внимание на вопросах, что такое мгновенное ускорение и скорость. Также рассмотрим, какими формулами можно определить эти величины.
Нахождение скорости
Об этом понятии известно каждому школьнику, начиная уже с младших классов. Все ученики знакомы с приведенной ниже формулой:
 Вам будет интересно:Геохимический барьер: определение термина, особенности
Вам будет интересно:Геохимический барьер: определение термина, особенности
v = S/t.
Здесь S - путь, который преодолело движущееся тело за время t. Данное выражение позволяет рассчитать некоторую среднюю скорость v. Действительно, нам ведь неизвестно, каким образом двигалось тело, на каком участке пути оно перемещалось быстрее, а на каком медленнее. Даже не исключена ситуация, что в некоторой точке пути оно находилось в состоянии покоя какое-то время. Единственное, что известно, это пройденный путь и соответствующий ему временной отрезок.
В старших классах школ скорость, как физическая величина, рассматривается в новом свете. Ученикам предлагают следующее ее определение:
v = dS/dt.
Чтобы понять это выражение, нужно знать, как вычисляется производная от некоторой функции. В данном случае - это S(t). Поскольку производная характеризует поведение кривой в данной конкретной точке, то вычисляемая по формуле выше скорость называется мгновенной.
Ускорение

Если механическое движение является переменным, то для его точного описания необходимо знать не только скорость, но и величину, которая показывает, как она изменяется во времени. Это - ускорение, которое является производная по времени скорости. А та, в свою очередь, есть производная по времени пути. Формула мгновенного ускорения имеет вид:
a = dv/dt.
Благодаря этому равенству можно определить изменение величины v в любой точке траектории.
По аналогии со скоростью, среднее ускорение вычисляется по такой формуле:
a = Δv/Δt.
Здесь Δv - это изменение модуля скорости тела за промежуток времени Δt. Очевидно, что в течение этого периода тело способно как ускоряться, так и замедляться. Величина a, определенная из выражения выше, покажет лишь в среднем быстроту изменения скорости.
Движение с постоянным ускорением
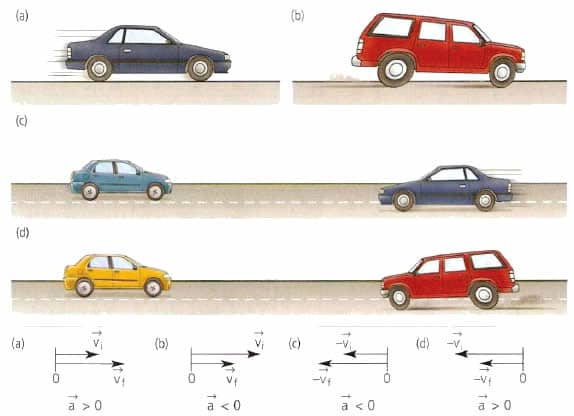
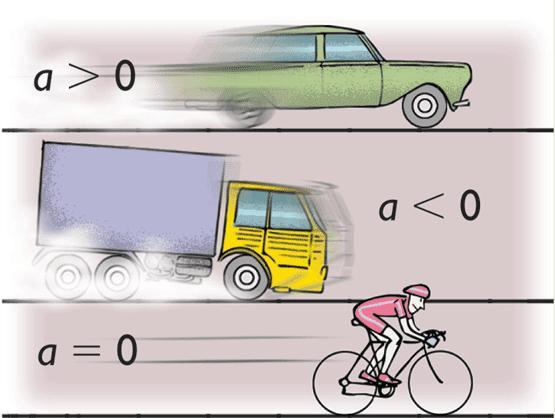
Отличительной особенностью этого типа перемещения тел в пространстве является постоянство величины а, то есть a=const.
Это движение также называют равноускоренным или равнозамедленным в зависимости от взаимного направления векторов скорости и ускорения. Ниже такое перемещение рассмотрим на примере двух наиболее распространенных траекторий: прямой линии и окружности.
При перемещении по прямой линии во время равноускоренного движения мгновенная скорость и ускорение, а также величина пройденного пути, связаны следующими равенствами:
v = v0 ± a*t;
S = v0*t ± a*t2/2.
Здесь v0 - это значение скорости, которым тело обладало до появления ускорения a. Заметим один нюанс. Для данного типа перемещения бессмысленно говорить о мгновенном ускорении, поскольку в любой точке траектории оно будет одним и тем же. Иными словами, мгновенная и средняя величины его будут равны друг другу.
Что касается скорости, то первое выражение позволяет определить ее в любой момент времени. То есть это будет мгновенный показатель. Для расчета средней скорости необходимо воспользоваться представленным выше выражением, то есть:
v = S/t = v0 ± a*(t1 + t2)/2.
Здесь t1 и t2 - это моменты времени, между которыми вычисляют среднюю скорость.
Знак "плюс" во всех формулах соответствует ускоренному передвижению. Соответственно знак "минус" - замедленному.
При изучении движения по окружности с постоянным ускорением в физике используют угловые характеристики, которые аналогичны соответствующим линейным. К ним относится угол поворота θ, угловая скорость и ускорение (ω и α). Эти величины связаны в равенства, аналогичные выражениям равноускоренного движения по прямой линии, которые приводятся ниже:
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2.
При этом угловые характеристики связаны с линейными следующим образом:
S = θ*R;
v = ω*R;
a = α*R.
Здесь R - радиус окружности.
Задача на определение среднего и мгновенного ускорения
Известно, что тело движется по сложной траектории. Его мгновенная скорость меняется по времени следующим образом:
v = 10 - 3*t + t3.
Чему равно мгновенное ускорение тела в момент t=3 (секунды)? Найти среднее ускорение за промежуток времени от двух до четырех секунд.
На первый вопрос задачи ответить несложно, если вычислить производную от функции v(t). Получаем:
a = |dv/dt|t=2;
а = |3*t2 - 3|t=2 = 24 м/с2.
Для определения среднего ускорения, следует воспользоваться таким выражением:
a = (v2 - v1)/(t2 - t1);
а = ((10 - 3*4 + 43) - (10 - 3*2 + 23))/2 = 25 м/c2.
Из расчетов следует, что среднее ускорение немного превышает мгновенное в середине рассмотренного временного промежутка.