Идеальный газ является удачной моделью в физике, которая позволяет изучать поведение реальных газов при различных условиях. В данной статье подробнее рассмотрим, что такое газ идеальный, формулой какой описывается его состояние, а также как рассчитывается его энергия.
Концепция газа идеального
Речь идет о газе, который образован частицами, не имеющими размера, и невзаимодействующими друг с другом. Естественно, что ни одна газовая система не удовлетворяет абсолютно точно отмеченным условиям. Тем не менее многие реальные текучие субстанции приближаются к этим условиям с точностью, достаточной для решения многих практических проблем.
 Вам будет интересно:Восточный Пакистан: история, факты и события
Вам будет интересно:Восточный Пакистан: история, факты и события
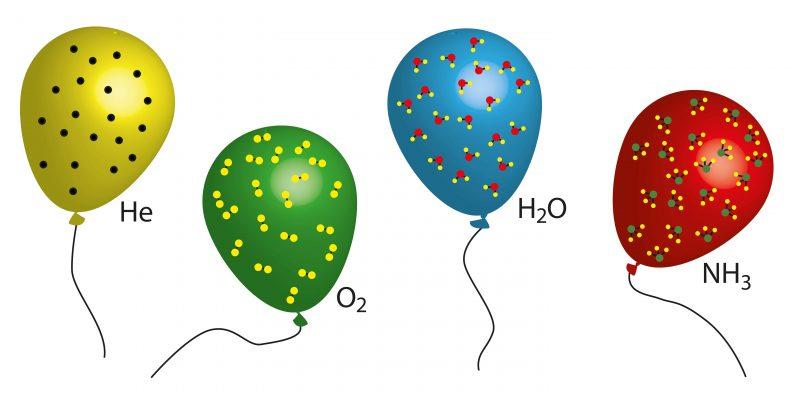
Если в газовой системе расстояние между частицами намного больше, чем их размеры, а потенциальная энергия взаимодействия намного меньше кинетической энергии поступательного и колебательного движений, то такой газ справедливо считать идеальным. Например, таковым является воздух, метан, газы благородные при невысоких давлениях и больших температурах. С другой стороны, водяной пар даже при низких давлениях не удовлетворяет концепции газа идеального, поскольку на поведение его молекул большое влияние оказывают водородные межмолекулярные взаимодействия.
Уравнение состояния газа идеального (формула)
Поведение газов человечество с использованием научного подхода изучает уже в течение нескольких веков. Первым прорывом в этой области стал закон Бойля-Мариотта, полученный экспериментально в конце XVII века. Спустя век были открыты еще два закона: Шарля и Гей Люссака. Наконец, в начале XIX века Амедео Авогадро, изучая различные чистые газы, сформулировал принцип, который теперь носит его фамилию.
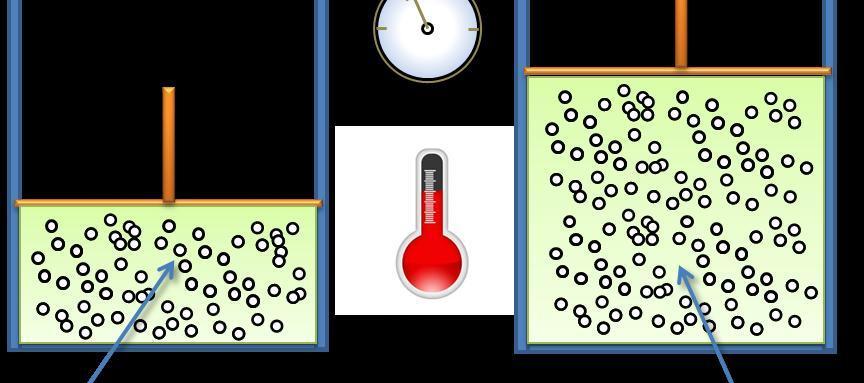
Все перечисленные выше достижения ученых привели Эмиля Клапейрона в 1834 году к написанию уравнения состояния газа идеального. Приведем это уравнение:
P × V = n × R × T.
Важность записанного равенства заключается в следующем:
- оно справедливо для любых идеальных газов независимо от их химического состава.
- оно связывает три основных термодинамических характеристики: температуру T, объем V и давление P.

Все названные выше газовые законы легко получить из уравнения состояния. Например, закон Шарля автоматически следует из закона Клапейрона, если положить величину P постоянной (изобарный процесс).
Универсальный закон также позволяет получить формулу для любого термодинамического параметра системы. Например, формула объема идеального газа запишется в виде:
V = n × R × T / P.
Молекулярно-кинетическая теория (МКТ)
Хотя универсальный газовый закон был получен чисто экспериментальным путем, в настоящее время существуют несколько теоретических подходов, приводящих к уравнению Клапейрона. Один из них заключается в использовании постулатов МКТ. В соответствии с ними, каждая частица газа движется по прямой траектории до тех пор, пока не встретит стенку сосуда. После абсолютно упругого столкновения с ней, она движется уже по другой прямой траектории, сохраняя кинетическую энергию, которую имела до столкновения.
Все частицы газа имеют скорости в соответствии со статистикой Максвелла-Больцмана. Важной микроскопической характеристикой системы является средняя скорость, которая сохраняется постоянной во времени. Благодаря этому факту удается рассчитать температуру системы. Соответствующая формула идеального газа имеет вид:
m × v2 / 2 = 3 / 2 × kB × T.
Где m - масса частицы, kB - константа Больцмана.
Из МКТ для идеального газа следует формула для абсолютного давления. Она имеет вид:
P = N × m × v2 / (3 × V).
Где N - число частиц в системе. С учетом предыдущего выражения, несложно перевести формулу для абсолютного давления в универсальное уравнение Клапейрона.
Внутренняя энергия системы
Согласно определению, идеальный газ обладает только кинетической энергией. Она же является его энергией внутренней U. Для газа идеального формулу энергии U можно получить, если умножить обе части равенства для кинетической энергии одной частицы на их число N в системе, то есть:
N × m × v2 / 2 = 3 / 2 × kB × T × N.
Тогда получаем:
U = 3 / 2 × kB × T × N = 3 / 2 × n × R × T.
Мы получили логичный вывод: внутренняя энергия прямо пропорциональна абсолютной температуре в системе. В действительности полученное выражение для U справедливо только для моноатомного газа, поскольку его атомы обладают лишь тремя поступательными степенями свободы (трехмерное пространство). Если же газ является двухатомным, тогда формула для U примет вид:
U2 = 5 / 2 × n × R × T.
Если система состоит из многоатомных молекул, тогда справедливо такое выражение:
Un>2 = 3 × n × R × T.
В последних двух формулах также учитываются вращательные степени свободы.
Пример задачи
Два моль гелия находятся в сосуде объемом 5 литров при температуре 20 oC. Необходимо определить давление и внутреннюю энергию газа.

Первым делом переведем все известные величины в СИ:
n = 2 моль;
V = 0,005 м3;
T = 293,15 К.
Давление гелия рассчитывается по формуле из закона Клапейрона:
P = n × R × T/V = 2 × 8,314 × 293,15 / 0,005 = 974 899,64 Па.
Рассчитанное давление равно 9,6 атмосферам. Так как гелий - газ благородный и одноатомный, то при таком давлении его можно считать идеальным.
Для одноатомного идеального газа формула для U имеет вид:
U = 3 / 2 × n × R × T.
Подставляя в нее значения температуры и количества вещества, получаем энергию гелия: U = 7311,7 Дж.
