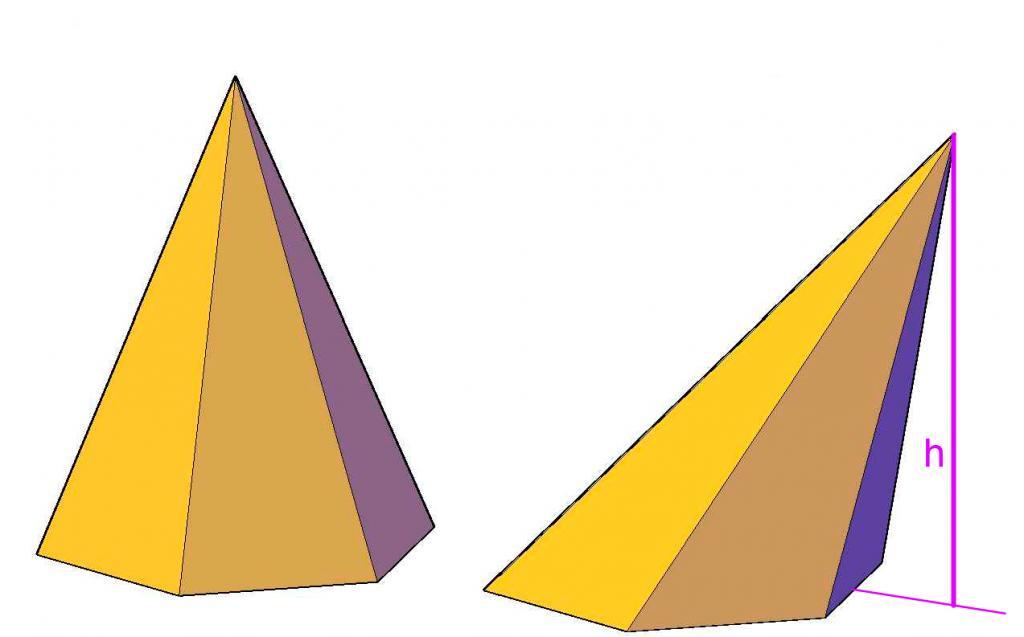
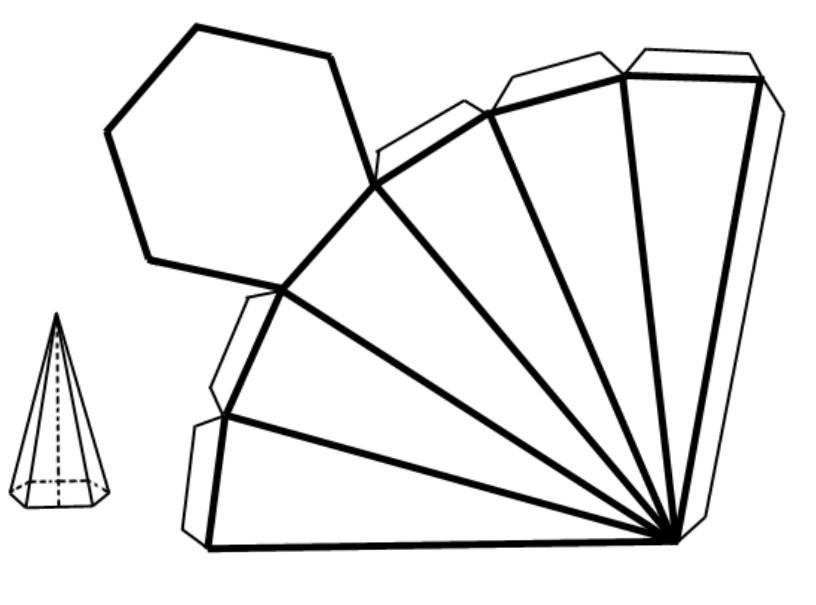
Одним из многогранников, которые изучают в школах в курсе пространственной геометрии, является пирамида. Эта фигура имеет ряд параметров и характеристик, для вычисления которых используют определенные математические формулы. Прочитав статью, вы узнаете, как находить площадь поверхности пирамиды.
Что представляет собой пирамида? Виды фигуры
Речь идет о фигуре в трехмерном пространстве, которая представляет собой многогранник, состоящий из треугольников и многоугольника. Если взять произвольный многоугольник на плоскости и соединить все его вершины прямыми отрезками с какой-нибудь точкой, не принадлежащей плоскости этого многоугольника, то мы получим пирамиду произвольного типа.
 Вам будет интересно:"Парирование" — это слово, значение которого нужно знать
Вам будет интересно:"Парирование" — это слово, значение которого нужно знать
Пирамида состоит из граней, вершин и ребер. Грани представляют собой плоскости, ограничивающие объем фигуры. Грани разделены друг от друга ребрами. Если три грани пересекаются в одной точке, то последняя является вершиной. Любая такая фигура имеет несколько вершин, например, у треугольной фигуры их четыре, а у четырехугольной - пять. У каждой пирамиды есть только одна вершина, которая не принадлежит основанию. Она называется главной или основной.
Класс пирамид включает несколько типов фигур. Пирамида будет прямой, если ее боковые треугольники являются равнобедренными. Если эти треугольники еще и равны друг другу, тогда фигура будет правильной. У любой прямой и правильной пирамиды высота (расстояние от главной вершины до основания) пересекает основание в его геометрическом центре. Кроме того, правильная фигура обладает равносторонним (равноугольным) основанием.
Площадь поверхности пирамиды
Под площадью любой подобной фигуры понимают сумму площадей всех ее сторон. Поскольку пирамиды имеют разный тип, то для расчета их площадей не существует универсальной формулы. Однако существуют выражения, которые могут быть использованы в каждом конкретном случае.
Какой бы не была пирамида, она всегда состоит из n-угольной грани и n треугольников. Площадь треугольников вычислить несложно, если известны их высоты и стороны основания. Что касается n-угольника, то для определения его площади следует провести анализ, что это за n-угольник, является ли он правильным, какие его углы известны. Универсальным методом определения его площади является разбиение на более простые фигуры, например, треугольники или параллелограммы.
Правильная фигура
Для правильной пирамиды формула площади поверхности давно уже определена. Прежде чем ее записывать, отметим, что площадь правильного основания фигуры может быть вычислена так:
Sn = n/4*a2*ctg(pi/n).
В формуле: a - сторона многоугольника, n - число сторон в нем. Например, для треугольника формула выглядит следующим образом:
S3 = √3/4*a2.
Для квадрата же получаем типичное равенство:
S4 = a2
Для правильной пирамиды площадь поверхности боковой Sb может быть определена по такой формуле:
Sb = n/2*hb*a.
Где hb - апофема пирамиды (высота бокового треугольника).
Складывая выражения для Sn и Sb, получаем формулу площади полной поверхности пирамиды:
S = Sn + Sb = n/4*a2*ctg(pi/n) + n/2*hb*a.
Отметим, для однозначного определения S любой пирамиды правильной необходимо знать два ее линейных параметра.
Наклонная фигура
Площадь поверхности пирамиды наклонной рассчитать гораздо сложнее, чем правильной. Тем не менее, зная ее развертку, всегда можно решить поставленную задачу. Боковая поверхность наклонной фигуры рассчитывается так:
Sb = 1/2*∑i=1n(ai*hbi).
Здесь ai - длина i-й стороны основания, hbi - длина i-й апофемы. Апофемы для наклонной пирамиды общего типа различаются.
Площадь основания So вычисляется, исходя из его типа, например, если это параллелограмм со сторонами a1 и a2 и углом между ними θ, тогда можно записать:
So = a1*a2*sin(θ).
Как для наклонной, так и для прямой пирамиды апофемы связаны с длинами боковых ребер и ребер основания. Эту связь часто используют при решении задач.