Все фигуры, которые ограничены гранями, находящимися в разных плоскостях в пространстве, обладают некоторым объемом. Вычислением этой величины занимается специальный геометрический раздел - стереометрия. В данной статье приведем формулу объема шестиугольной призмы.
Что такое призма?
Очевидно, что прежде чем находить объем геометрической фигуры, следует познакомиться с ней и понять, какими свойствами она обладает. В данном случае речь идет о призме. В стереометрии для этой фигуры приводится следующее определение: призмой называется любой пространственный геометрический объект, который ограничен двумя n-угольниками, находящимися в параллельных плоскостях, и n параллелограммами. Здесь n - любое натуральное число начиная с трех.
 Вам будет интересно:Структурный гетерохроматин - это что такое?
Вам будет интересно:Структурный гетерохроматин - это что такое?
Построить фигуру несложно. Для этого следует взять произвольный многоугольник и с помощью одинаковых параллельных друг другу отрезков перенести его в другую плоскость. Получившаяся фигура будет призмой. Отметим, что она, в отличие от конуса, цилиндра и сферы, не является фигурой вращения, то есть ее нельзя получить с помощью вращения вокруг оси какой-либо плоской фигуры.

 Вам будет интересно:Социально-значимая деятельность: определение, особенности, развитие и примеры
Вам будет интересно:Социально-значимая деятельность: определение, особенности, развитие и примеры
Выше на рисунке приведен для примера параллелепипед, который является четырехугольной призмой.
Призма шестиугольная и ее виды
Далее в статье приведем формулу объема призмы шестиугольной. Что представляет собой эта фигура? Любая призма, имеющая в основании шестиугольник, называется шестиугольной.
Она образована двумя шестиугольниками в основаниях и шестью параллелограммами, совокупность которых составляет боковую площадь фигуры. Эта призма имеет 12 вершин, 8 граней или сторон и 18 ребер, 2/3 из которых принадлежат основаниям.
Приведенному описанию элементов соответствуют несколько видов шестиугольной призмы. Во-первых, эта фигура может быть выпуклой или вогнутой, что зависит от шестиугольника в основаниях, во-вторых, призма может быть наклонной и прямой. Разница между ними заключается в том, что в прямой фигуре любая боковая сторона будет перпендикулярна основаниям, а в наклонной фигуре боковые стороны пересекают основания под некоторыми углами, которые отличны от 90o. Обе призмы показаны на рисунке.
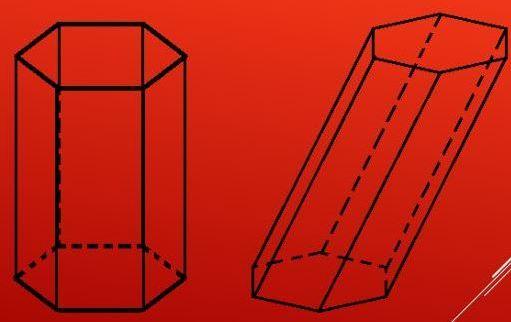
Заметим, что условие перпендикулярности боковых сторон и оснований приводит к тому, что параллелограммы прямой призмы становятся прямоугольниками.
Наконец, в-третьих, шестиугольная призма бывает правильной и неправильной. Последней будет любая фигура, которая не является прямой и не обладает правильным шестиугольным основанием. Далее основное внимание будем уделять именно правильной призме.
Правильный шестиугольник
Для определения объемов геометрических фигур многих классов необходимо знать значение площади их основания. Этот факт справедлив для пирамид, цилиндров, конусов. Призмы тоже не являются исключением.
Чтобы найти площадь основания шестиугольной призмы, следует рассчитать площадь шестиугольника. Проще всего сделать это для правильной фигуры. Для наглядности покажем, что такое правильный шестиугольник.
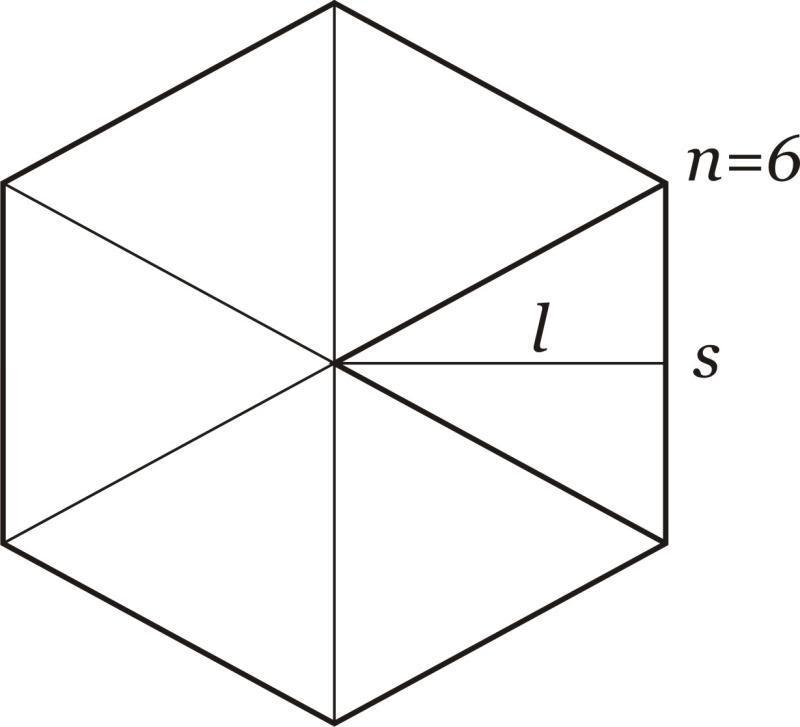
Видно, что представляет он многоугольник, образованный шестью одинаковыми сторонами, которые пересекаются под углами 120o. Также видно, что в шестиугольник можно вписать окружность некоторого радиуса, а также можно описать его окружностью.
Вычисление площади основания призмы шестиугольной правильной сводится к определению площади приведенной выше фигуры. Если шестиугольник разбить на равносторонние треугольники так, как показано на рисунке, то его площадь будет равна умноженной на 6 площади одного треугольника. Обозначим длину стороны шестиугольника буквой a, тогда для площади S шестиугольника получаем:
S = 6*1/2*a*√3/2*a = 3*√3/2*a2.
Для любого другого шестиугольника, который не является правильным, эта формула будет несправедливой.
Формула объема шестиугольной призмы
Вычислить объем любой призмы несложно, для этого следует знать всего два ее параметра: высоту h и основания площадь S. Расчет объема V осуществляется по следующей формуле:
V = h*S.
Отметим важную вещь: записанное выражение справедливо для любых видов призм, включая вогнутые и наклонные. Тем не менее для произвольной призмы, несмотря на простоту формулы, применять ее бывает сложно. Сложность связана с определением обоих параметров в выражении.
В связи с вышесказанным, рассмотрим конкретную правильную призму с правильным шестиугольным основанием. Если ее высота равна h, а длина стороны равна a, тогда формула объема шестиугольной призмы правильной примет вид:
V = 3*√3/2*h*a2.
При записи этого выражения была подставлена формула для S, приведенная в предыдущем пункте.
Далее решим две задачи, в которых покажем, как найти объем шестиугольной призмы для конкретных случаев.
Задача с известной диагональю
Ниже на рисунке показана правильная призма. Известно, что сторона ее основания равна 9 см. Чему равен объем шестиугольной призмы, если диагональ AB имеет длину 21 см.
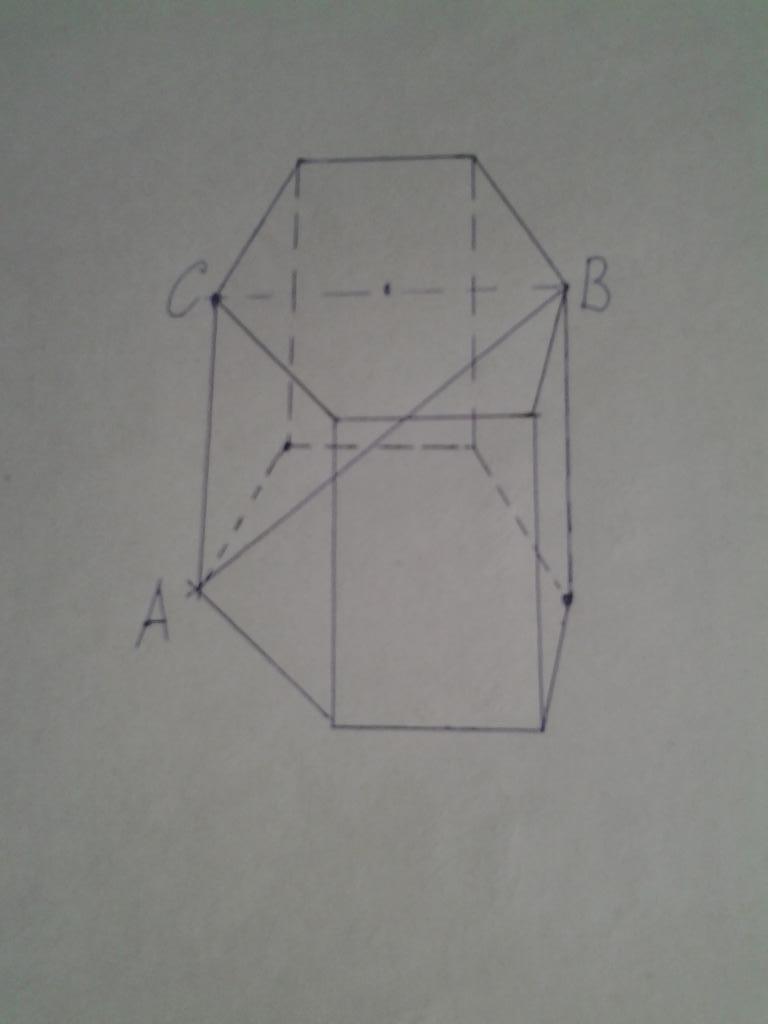
Не сложно догадаться, взглянув на рисунок, что треугольник ABC является прямоугольным, причем сторона AB - это гипотенуза. Катет AC является высотой h фигуры. Чтобы вычислить объем призмы, нам необходимо найти длину этого катета. Заметим, что второй катет CB имеет в два раза большую длину, чем сторона основания, то есть 18 см. Применяем теорему Пифагора и получаем:
h = AC = √(AB2-CB2) = √(212-182) ≈ 10,82 см.
Значение высоты мы округлили до сотых долей сантиметра.
Поскольку нам известна высота h и сторона основания a, то можно применить формулу для V. Получаем:
V = 3*√3/2*h*a2 = 3*√3/2*10,82*92 = 2277 см3.
Таким образом, рассмотренная призма имеет объем почти 2,3 литра.
Задача с вписанным в призму цилиндром
Известно, что цилиндр с радиусом 12 см вписан в правильную шестиугольную призму. Объем цилиндра равен 1360 см3. Чему равен объем призмы?

Как было показано, определить объем призмы можно, если знать ее высоту и сторону основания. Начнем с определения стороны. Поскольку радиус r окружности, вписанной в шестиугольник, известен, значит, длину стороны a можно рассчитать так:
a = 2*r/√3.
Понять, откуда взялась эта формула, можно, если учесть, что радиус r является высотой одного из шести равносторонних треугольников шестиугольника.
Теперь вычислим высоту h призмы. Согласно условию задачи, она должна совпадать с высотой цилиндра. Объем же цилиндра рассчитывается по той же формуле, что и для призмы. Имеем:
Vc = So*h = pi*r2*h =>
h = Vc/(pi*r2).
Подставляем выражения для a и h в формулу для V призмы, получаем:
V = 3*√3/2*h*a2 = 3*√3/2*Vc/(pi*r2)*(2*r/√3)**2 = 2*√3*Vc/pi.
Мы пришли к интересному результату: оказывается, объем шестиугольной призмы не зависит от радиуса вписанного цилиндра, а однозначно определяется его объемом. Подставив значение Vc, получаем объем призмы, равный приблизительно 1500 см3.
