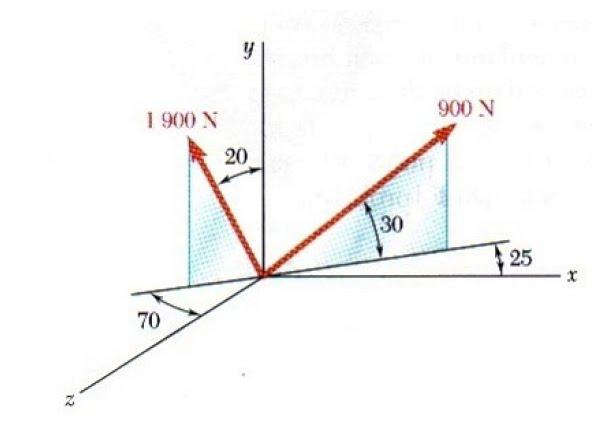
- Сила и ее физический смысл
- Какие силы бывают
- Сила - векторная величина
- Что такое проекция силы на ось
- Углы между силой и ее проекциями на координатные оси
- Сила и ее проекции на плоскости координат
- Углы между проекциями на плоскость и вектором силы
- Где используются проекции сил
- Задача на определение проекций силы на плоскости и на оси координат
- Задача со скользящим бруском по наклонной плоскости
Сила - это одно из важных понятий в физике. Она является причиной изменения состояния любых объектов. В данной статье рассмотрим, что собой представляет эта величина, какие силы бывают, а также покажем, как находить проекцию силы на ось и на плоскость.
Сила и ее физический смысл
В физике сила - это векторная величина, которая показывает изменение количества движения тела за единицу времени. Данное определение полагает силу динамической характеристикой. С точки зрения же статики сила в физике - это мера упругой или пластической деформации тел.
 Вам будет интересно:Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Вам будет интересно:Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Международная система СИ выражает силу в ньютонах (Н). Что такое 1 ньютон, проще всего понять на примере второго закона классической механики. Математическая запись его следующая:
F¯ = m*a¯
Здесь F¯ - некоторая внешняя сила, действующая на тело массой m, и приводящая к ускорению a¯. Из формулы следует количественное определение одного ньютона: 1 Н - это такая сила, которая приводит к изменению скорости тела массой 1 кг на 1 м/с за каждую секунду.

 Вам будет интересно:Предположение — это и высказанная вслух мысль, и основа прогресса
Вам будет интересно:Предположение — это и высказанная вслух мысль, и основа прогресса
Примерами динамического проявления силы являются ускорение автомобиля или свободно падающего тела в гравитационном земном поле.
Статическое проявление силы, как было отмечено, связано с явлениями деформации. Здесь следует привести следующие формулы:
F = P*S
F = -k*x
Первое выражение связывает силу F с давлением P, которое она оказывает на некоторую площадку S. Через эту формулу 1 Н можно определить как давление в 1 паскаль, прилагаемое к площадке 1 м2. Например, столб атмосферного воздуха на уровне моря давит на площадку 1 м2 с силой 105 Н!
Второе выражение является классической формой записи закона Гука. Например, растяжение или сжатие пружины на линейную величину x приводит к возникновению противодействующей силы F (в выражении k - коэффициент пропорциональности).
Какие силы бывают
Выше уже было показано, что силы могут быть статические и динамические. Здесь скажем, что помимо этой их особенности, они могут быть силами контакта или дальнодействующие. Например, сила трения, реакции опоры - это контактные силы. Причина их появления заключается в справедливости принципа Паули. Последний гласит, что два электрона не могут занимать одно и то же состояние. Именно поэтому прикосновение двух атомов приводит к их отталкиванию.
 Вам будет интересно:Определение призмы, ее элементы и виды. Основные характеристики фигуры
Вам будет интересно:Определение призмы, ее элементы и виды. Основные характеристики фигуры
Дальнодействующие силы появляются в результате взаимодействия тел через некоторое поле-носитель. Например, такими являются сила гравитации или электромагнитное взаимодействие. Обе силы имеют бесконечный радиус действия, однако, их интенсивность падает, как квадрат расстояния (законы Кулона и всемирного тяготения).
Сила - векторная величина
Разобравшись со смыслом рассматриваемой физической величины, можно перейти к изучению вопроса проекции силы на ось. В первую очередь заметим, что данная величина является векторной, то есть она характеризуется модулем и направлением. Покажем, как рассчитывать модуль силы и ее направление.
Известно, что любой вектор можно задать однозначно в данной системе координат, если известны значения координат его начала и конца. Предположим, что имеется некоторый направленный отрезок MN¯. Тогда его направление и модуль можно определить с помощью следующих выражений:
MN¯ = (x2-x1; y2-y1; z2-z1);
|MN¯| = √((x2-x1)2 + (y2-y1)2 + (z2-z1)2).
Здесь координаты с индексами 2 соответствуют точке N, с индексами 1 - точке M. Вектор MN¯ направлен из M в N.
Для общности мы показали, как находить модуль и координаты (направление) вектора в трехмерном пространстве. Аналогичные формулы без третьей координаты справедливы для случая на плоскости.
Таким образом, модуль силы - это ее абсолютная величина, выраженная в ньютонах. С точки зрения геометрии, модуль - это длина направленного отрезка.
Что такое проекция силы на ось?
Речь о проекциях направленных отрезков на координатные оси и плоскости удобнее всего вести, если предварительно расположить соответствующий вектор в начале координат, то есть в точке (0; 0; 0). Предположим, что у нас имеется некоторый вектор силы F¯. Поместим его начало в точку (0; 0; 0), тогда координаты вектора можно записать так:
F¯ = ((x1 - 0); (y1 - 0); (z1 - 0)) = (x1; y1; z1).
Вектор F¯ показывает направление силы в пространстве в данной координатной системе. Теперь проведем перпендикулярные отрезки из конца F¯ к каждой из осей. Расстояние от точки пересечения перпендикуляра с соответствующей осью до начала координат называется проекцией силы на ось. Не трудно догадаться, что в случае с силой F¯ ее проекции на оси x, y и z будут равны x1, y1 и z1, соответственно. Заметим, что эти координаты показывают модули проекций силы (длину отрезков).
Углы между силой и ее проекциями на координатные оси
 Вам будет интересно:Круглый прямой цилиндр, развертка и формула для ее площади
Вам будет интересно:Круглый прямой цилиндр, развертка и формула для ее площади
Вычисление этих углов не является сложной задачей. Все, что требуется для ее решения, - это знание свойств тригонометрических функций и умение применять теорему Пифагора.
Например, определим угол между направлением силы и ее проекцией на ось x. Соответствующий прямоугольный треугольник будет образован гипотенузой (вектор F¯) и катетом (отрезок x1). Второй катет - это дистанция от конца вектора F¯ до оси x. Угол α между F¯ и осью x вычисляется по формуле:
α = arccos(|x1|/|F¯|) = arccos(x1/√(x12+y12+z12)).
Как видим, для определения угла между осью и вектором необходимо и достаточно знать координаты конца направленного отрезка.
Для углов с другими осями (y и z) можно записать аналогичные выражения:
β = arccos(|y1|/|F¯|) = arccos(y1/√(x12+y12+z12));
γ = arccos(|z1|/|F¯|) = arccos(z1/√(x12+y12+z12)).
Заметим, что во всех формулах стоят модули в числители, что исключает появление тупых углов. Между силой и ее осевыми проекциями углы всегда меньше или равны 90o.
Сила и ее проекции на плоскости координат
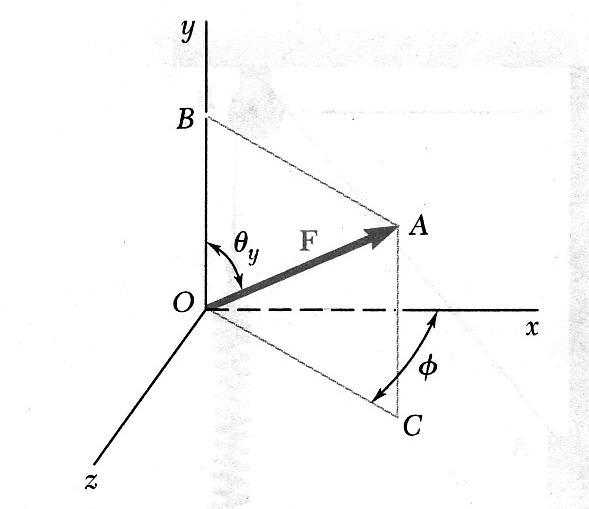
Определение проекции силы на плоскость не отличается от такового для оси, только в данном случае перпендикуляр следует опускать не на ось, а на плоскость.
В случае пространственной прямоугольной системы координат мы имеем три взаимно перпендикулярные плоскости xy (горизонтальная), yz (фронтальная вертикальная), xz (боковая вертикальная). Точки пересечения опущенных из конца вектора перпендикуляров к названным плоскостям равны:
(x1; y1; 0) для xy;
(x1; 0 ; z1) для xz;
(0 ; y1; z1) для zy.
Если каждую из отмеченных точек соединить с началом координат, то мы получим проекцию силы F¯ на соответствующую плоскость. Чему равен модуль силы, мы знаем. Чтобы найти модуль каждой проекции, необходимо применить теорему Пифагора. Обозначим проекции на плоскости как Fxy, Fxz и Fzy. Тогда для их модулей будут справедливы равенства:
Fxy = √(x12+y12);
Fxz = √(x12+ z12);
Fzy = √(y12+ z12).
Углы между проекциями на плоскость и вектором силы
В пункте выше были приведены формулы для модулей проекций на плоскость рассматриваемого вектора F¯. Эти проекции вместе с отрезком F¯ и расстоянием от его конца до плоскости образуют прямоугольные треугольники. Поэтому, как и в случае с проекциями на ось, можно воспользоваться определением тригонометрических функций, чтобы вычислить рассматриваемые углы. Можно записать следующие равенства:
α = arccos(Fxy /|F¯|) = arccos(√(x12+y12) /√(x12+y12+z12));
β = arccos(Fxz/|F¯|) = arccos(√(x12+z12)/√(x12+y12+z12));
γ = arccos(Fzy/|F¯|) = arccos(√(y12+z12)/√(x12+y12+z12)).
Важно понимать, что угол между направлением силы F¯ и соответствующей ее проекцией на плоскость равен углу между F¯ и этой плоскостью. Если рассматривать эту задачу с точки зрения геометрии, то можно сказать, что направленный отрезок F¯ является наклонной по отношению к плоскостям xy, xz и zy.
Где используются проекции сил?
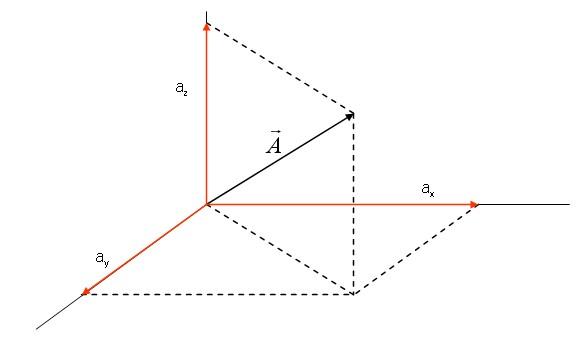
Приведенные формулы для проекций силы на оси координат и на плоскости представляют не только теоретический интерес. Они часто используются при решении физических задач. Сам процесс нахождения проекций называется разложением силы на ее составляющие. Последние представляют собой вектора, сумма которых должна дать исходный вектор силы. В общем случае можно разложить силу на произвольные составляющие, однако, для решения задач удобно пользоваться именно проекциями на перпендикулярные оси и плоскости.
Задачи, где применяются понятие проекций сил, могут быть самыми разными. Например, тот же второй закон Ньютона предполагает, что внешняя сила F¯, действующая на тело, должна быть направлена так же, как вектор скорости v¯. Если их направления различаются на некоторый угол тогда, чтобы равенство оставалось справедливым, подставлять в него следует уже не саму силу F¯, а ее проекцию на направление v¯.
Далее приведем пару примеров, где покажем, как пользоваться записанными формулами.
Задача на определение проекций силы на плоскости и на оси координат
Предположим, что имеется некоторая сила F¯, которая представлена вектором, имеющим следующие координаты конца и начала:
(2; 0; 1);
(-1; 4; -1).
Необходимо определить модуль силы, а также все ее проекции на координатные оси и плоскости и углы между F¯ и каждой ее проекцией.
Начнем решать задачу с вычисления координат вектора F¯. Имеем:
F¯ = (-1; 4; -1) - (2; 0; 1) = (-3; 4; -2).
Тогда модуль силы будет равен:
|F¯| = √(9 + 16 + 4) = √29 ≈ 5,385 Н.
Проекции на оси координат равны соответствующим координатам вектора F¯. Рассчитаем углы между ними и направлением F¯. Имеем:
α = arccos(|-3 |/5,385) ≈ 56,14o;
β = arccos(|4|/5,385) ≈ 42,03o;
γ = arccos(|-2|/5,385) ≈ 68,20o.
Поскольку координаты вектора F¯ известны, можно рассчитать модули проекций силы на плоскости координат. Пользуясь приведенными выше формулами, получаем:
Fxy = √(9 +16 ) = 5 Н;
Fxz = √(9 + 4 ) = 3,606 Н;
Fzy = √(16 + 4 ) = 4,472 Н.
Наконец, остается вычислить углы между найденными проекциями на плоскость и вектором силы. Имеем:
α = arccos(Fxy /|F¯|) = arccos(5/5,385) ≈ 21,8o;
β = arccos(Fxz/|F¯|) = arccos(3,606/5,385) ≈ 48,0o;
γ = arccos(Fzy/|F¯|) = arccos(4,472/5,385) ≈ 33,9o.
Таким образом, вектор F¯ ближе всего наклонен к координатной плоскости xy.
Задача со скользящим бруском по наклонной плоскости

Теперь решим физическую задачу, где необходимо будет применить концепцию проекции силы. Пусть дана деревянная наклонная плоскость. Угол ее наклона к горизонту равен 45o. На плоскости находится деревянный брусок, имеющий массу 3 кг. Необходимо определить, с каким ускорением будет перемещаться этот брусок по плоскости вниз, если известно, что коэффициент трения скольжения равен 0,7.
Для начала составим уравнение движения тела. Поскольку на него будут действовать всего две силы (проекция силы тяжести на плоскость и сила трения), то уравнение примет вид:
Fg - Ff = m*a =>
a = (Fg - Ff)/m.
Здесь Fg, Ff - проекция силы тяжести и сила трения, соответственно. То есть задача сводится к вычислению их значений.
Поскольку угол, под которым плоскость наклонена к горизонту, равен 45o, то несложно показать, что проекция силы тяжести Fg вдоль поверхности плоскости будет равна:
Fg = m*g*sin(45o) = 3*9,81/√2 ≈ 20,81 Н.
Эта проекция силы стремится вывести из состояния покоя деревянный брусок и придать ему ускорение.
Согласно определению, сила трения скольжения равна:
Ff = μ*N
Где μ = 0,7 (см. условие задачи). Сила реакции опоры N равна проекции силы тяжести на ось, перпендикулярную наклонной плоскости, то есть:
N = m*g*cos(45o)
Тогда сила трения равна:
Ff = μ*m*g*cos(45o) = 0,7*3*9,81/√2 ≈ 14,57 Н.
Подставляем найденные силы в уравнение движения, получаем:
a = (Fg - Ff)/m = (20,81 - 14,57)/3 = 2,08 м/с2.
Таким образом, брусок будет спускаться по наклонной плоскости, увеличивая за каждую секунду свою скорость на 2,08 м/с.