Вычисление объемов пространственных фигур является одной из важных задач стереометрии. В данной статье рассмотрим вопрос определения объема такого полиэдра, как пирамида, а также приведем формулу объема пирамиды шестиугольной правильной.
Пирамида шестиугольная
Для начала рассмотрим, что собой представляет фигура, о которой пойдет речь в статье.
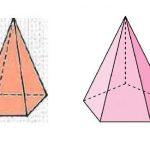
Пусть у нас имеется произвольный шестиугольник, стороны которого не обязательно равны друг другу. Также предположим, что мы выбрали в пространстве точку, не находящуюся в плоскости шестиугольника. Соединив все углы последнего с выбранной точкой, мы получим пирамиду. Две разные пирамиды, имеющие шестиугольное основание, показаны на рисунке ниже.
 Вам будет интересно:Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Вам будет интересно:Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
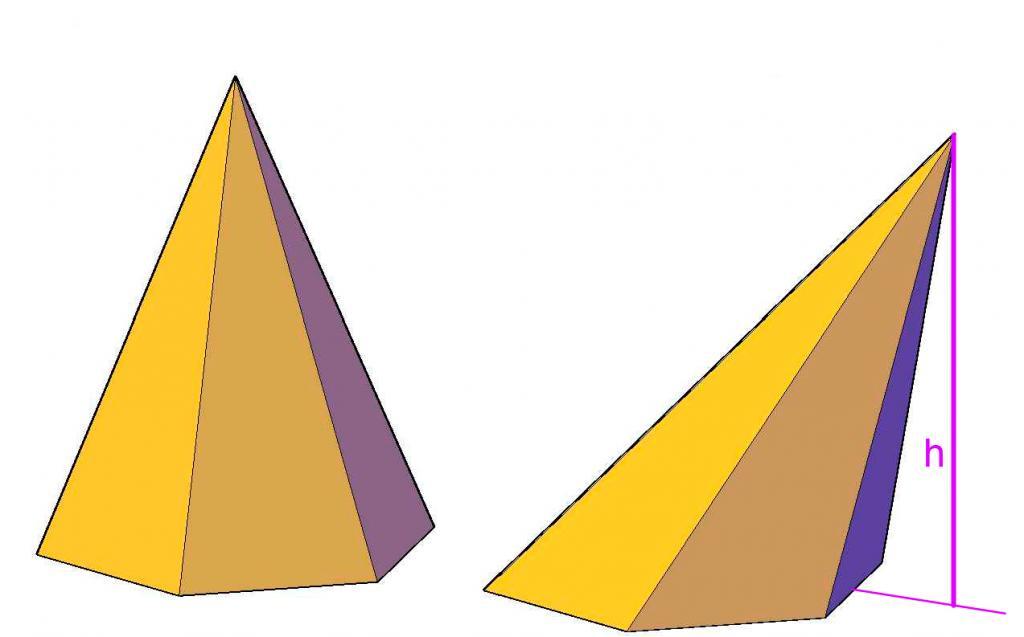
Видно, что помимо шестиугольника фигура состоит из шести треугольников, точка соединения которых называется вершиной. Различие между изображенными пирамидами заключается в том, что высота h правой из них не пересекает шестиугольное основание в его геометрическом центре, а высота левой фигуры попадает точно в этот центр. Благодаря этому критерию левая пирамида получила название прямой, а правая - наклонной.
Поскольку основание левой фигуры на рисунке образовано шестиугольником с равными сторонами и углами, то она называется правильной. Дальше в статье речь пойдет только об этой пирамиде.
Объем шестиугольной пирамиды
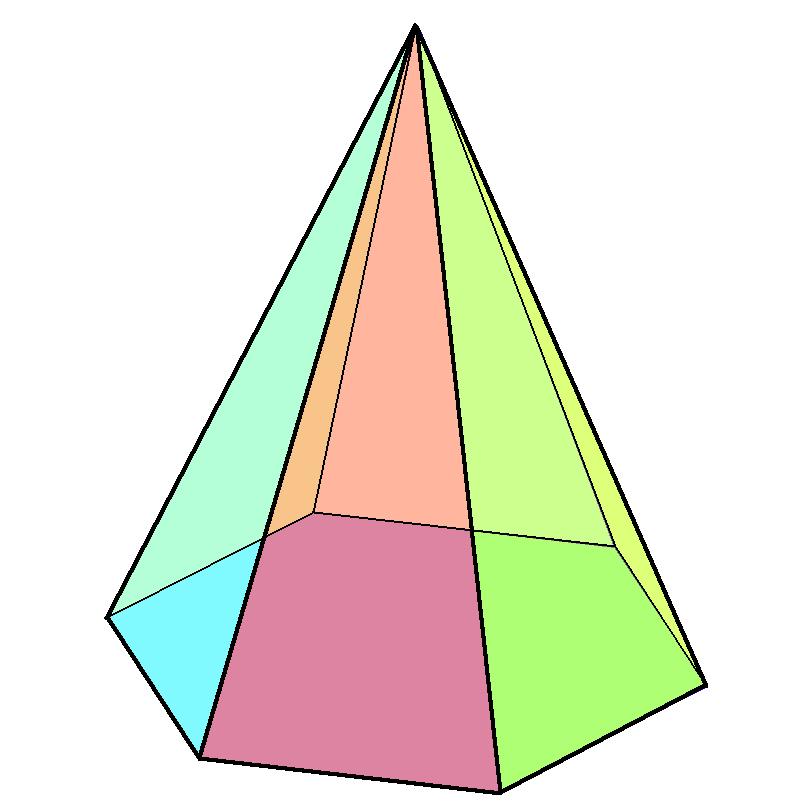
Для вычисления объема произвольной пирамиды справедлива следующая формула:
V = 1/3 * h * So
Здесь h - это длина высоты фигуры, So - площадь ее основания. Воспользуемся этим выражением для определения объема пирамиды шестиугольной правильной.
Поскольку в основании рассматриваемой фигуры лежит равносторонний шестиугольник, то для вычисления его площади можно воспользоваться следующим общим выражением для n-угольника:
Sn = n/4 * a2 * ctg(pi/n)
Здесь n - целое число, равное количеству сторон (углов) многоугольника, a - длина его стороны, функцию котангенса высчитывают, используя соответствующие таблицы.
Применяя выражение для n = 6, получим:
S6 = 6/4 * a2 * ctg(pi/6) = √3/2 * a2
Теперь остается подставить это выражение в общую формулу для объема V:
V6 = S6 * h = √3/2 * h * a2
Таким образом, для вычисления объема рассматриваемой пирамиды необходимо знать два ее линейных параметра: длину стороны основания и высоту фигуры.
Пример решения задачи
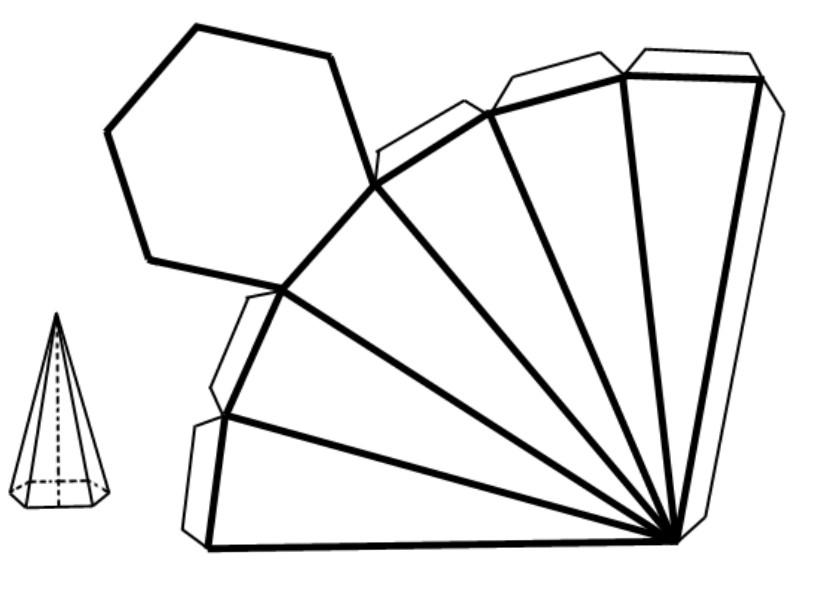
Покажем, как можно использовать полученное выражение для V6 для решения следующей задачи.
Известно, что правильной шестиугольной пирамиды объем равен 100 см3. Необходимо определить сторону основания и высоту фигуры, если известно, что они связаны друг с другом следующим равенством:
a = 2*h
Поскольку в формулу для объема входят только a и h, то можно подставить в нее любой из этих параметров, выраженный через другой. Например, подставим a, получаем:
V6 = √3/2*h*(2*h)2 =>
h = ∛(V6/(2*√3))
Для нахождения значения высоты фигуры необходимо взять корень третей степени из объема, что соответствует размерности длины. Подставляем значение объема V6 пирамиды из условия задачи, получаем высоту:
h = ∛(100/(2*√3)) ≈ 3,0676 см
Поскольку сторона основания в соответствии с условием задачи в два раза больше найденной величины, то получаем значение для нее:
a = 2*h = 2*3,0676 = 6,1352 см
Объем шестиугольной пирамиды можно найти не только через высоту фигуры и значение стороны ее основания. Достаточно знать два разных линейных параметра пирамиды для его вычисления, например апотему и длину бокового ребра.
