Математика и физика являются, пожалуй, двумя научными дисциплинами, которые ближе всего связаны друг с другом. Так, результаты одной из них используются для развития другой. Одним из ярких примеров, отражающих их взаимодействие, является расчет момента инерции прямоугольника относительно оси.
О моменте инерции в математике и физике
Многие люди, знакомые с физикой или математикой, наверняка, слышали об этом понятии. Тем не менее, стоит разобраться в нем подробнее, чтобы не возникало путаницы.
 Вам будет интересно:Астрология - это наука о чем? Доводы за и против, объект изучения
Вам будет интересно:Астрология - это наука о чем? Доводы за и против, объект изучения
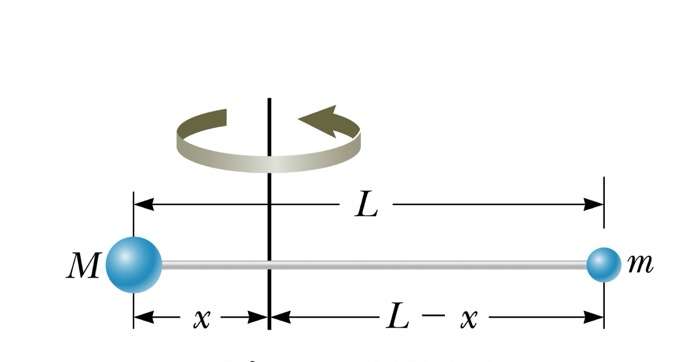
В физике под моментом инерции понимают характеристику вращающейся системы, которая описывает инерционные свойства тела. Например, для точки с массой m, которая совершает круговые движения вокруг оси, находящейся от нее на расстоянии r, эта величина выражается формулой:
I = m*r2.
Откуда видно, что описывается она килограммами на квадратный метр.
В математике момент инерции - это совершенно иная вещь, которая вычисляется не относительно трехмерного объекта, а относительно плоского тела или сечения. В общем случае можно говорить о моменте инерции n-го порядка. В данной же статье, при вычислении момента инерции прямоугольника, речь пойдет о величине второго порядка.
Момент инерции 2-го порядка для сечения
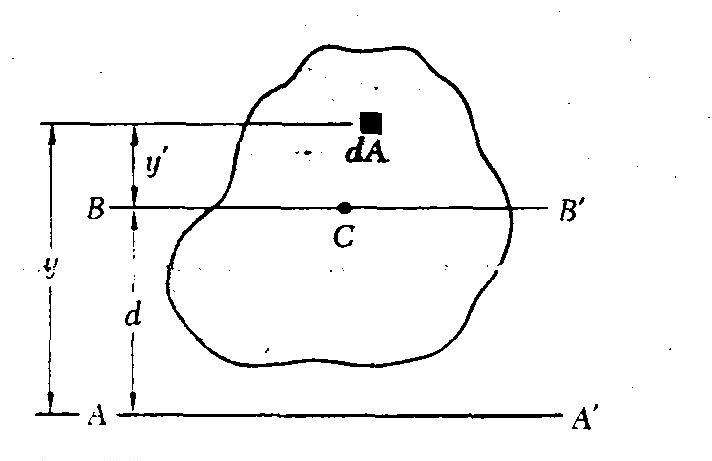
Стоит перейти к математической формулировке рассматриваемой величины. Итак, в математике она появляется в виде следующего определения:
Io = ∫∫A(r2*dA).
Здесь Io - момент инерции второго порядка, вычисляемый относительно оси O; A - площадь сектора, для которого определяется величина Io; dA - элемент площади сектора, который находится от оси O на расстоянии r.
Эта формула показывает, что размерностью Io является единица расстояния в четвертой степени (м4), что отличает его от момента инерции для тела в физике (см. пункт выше).
Зачем вычисляют величину Io? Конечно же, это не чистая математическая задача, которая не имеет прикладного характера. Момент инерции Io для сечений различной формы необходим при расчетах сгибающих напряжений в инженерных конструкциях, например, для балок.

Далее приведены расчеты для осевого момента инерции прямоугольника при различном положении оси вращения O относительно объекта.
Ось проходит через центр фигуры параллельно одной из сторон
Пусть дан прямоугольник с размерами сторон a и b. Допустим, что ось O делит фигуру на две равные половины и параллельна стороне a. Эта ситуация изображена на рисунке ниже.
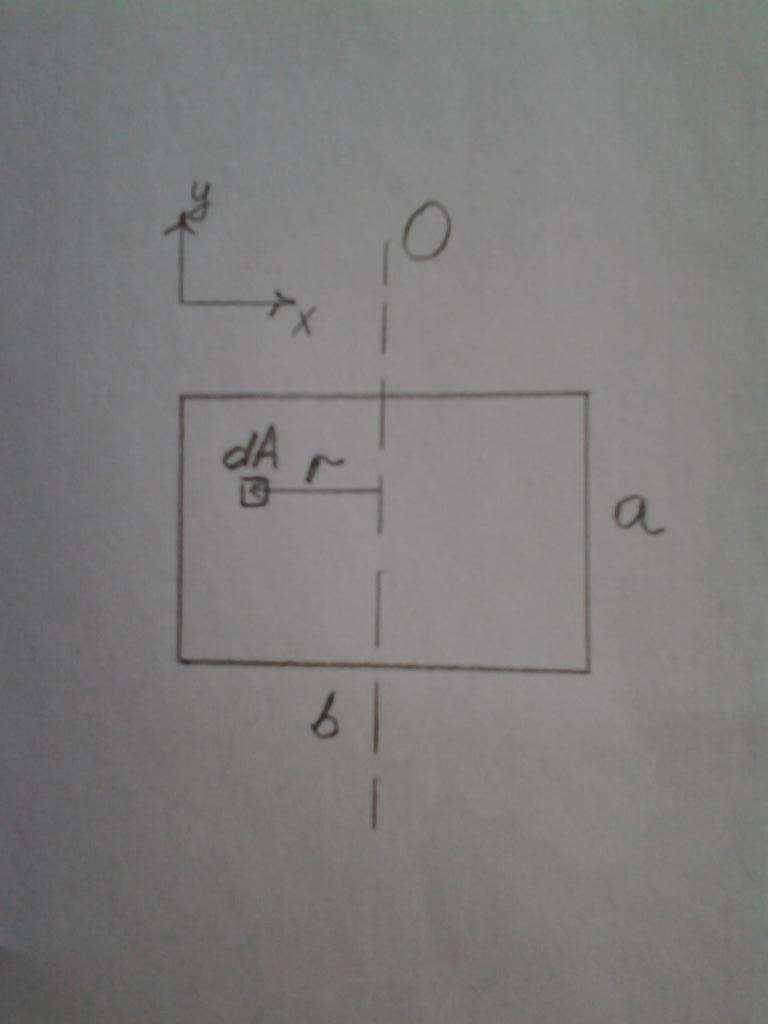
Двойной интеграл для такой ситуации можно посчитать достаточно просто, поскольку расстояние r любого элемента с площадью dA будет равно x. При этом интегрирование проводится от -b/2 до +b/2 (ось O пересекает начало координат по оси x). Что касается пределов интегрирования по y, то их можно выбрать, как от -a/2 до +a/2 (начало координат в центре фигуры), так и от 0 до a (начало координат лежит на середине одной из сторон длиной b). Для определенности стоит выбрать второй вариант. Тогда общая формула для момента инерции второго порядка запишется в виде:
Io = ∫0a∫-b/2+b/2(x2*dx*dy).
Вычисляем двойной интеграл по порядку, подставляем известные пределы, получается:
Io = x3/3|-b/2+b/2*y|0a = b3*a/12.
Таким образом, получена формула момента инерции прямоугольника для оси, проходящей через его середину параллельно сторонам с длиной a.
Очевидно, что если ось будет проходить параллельно сторонам b, то ничего не изменится в расчете, за исключением того, что обозначения сторон поменяются местами. То есть получится формула:
Io = a3*b/12.
Ось проходит через сторону прямоугольника
В этом случае ситуация полностью аналогична предыдущей, только теперь ось O1 сдвинута к одному из краев фигуры. Для расчета такого момента инерции необходимо лишь поменять пределы интегрирования по соответствующей стороне.
Пусть ось O1 будет проходить через сторону a, тогда пределы интегрирования по x будут от 0 до b. Если подставить их в формулу, получится:
Io1 = x3/3|0b*y|0a = b3*a/3.
Соответственно, если ось O1 проходит через b, тогда получится:
Io1 = a3*b/3.
Как видно, смещение оси к краю фигуры приводит к увеличению ее момента инерции в 4 раза.
Стоит отметить, что формулы для случая, рассмотренного в данном пункте, можно было получить с использованием теоремы Штейнера, которая имеет аналогичный вид, что и в случае расчета момента инерции тела в физике:
Io1 = Io + d2*A.
Здесь d - расстояние между осями O и O1. Если обе оси параллельны сторонам a фигуры, тогда d = b/2 (половина длины стороны b прямоугольника). Поскольку площадь прямоугольника равна a*b, то получится:
Io1 = b3*a/3 + (b/2)2*a*b = b3*a/12 + b3*a/4 = b3*a/3.
Таким же образом применяется эта теорема для оси O1, параллельной стороне b, только d в этом случае будет равен уже a/2.
