Среди всех последовательностей чисел геометрическая прогрессия, которую рассматривают в курсе алгебры 9 класса, является одной из самых известных. Что она собой представляет и как решить геометрическую прогрессию — на эти вопросы дан ответ в данной статье.
Последовательность чисел, которая подчиняется математическому закону
Название этого пункта является общим определением геометрической прогрессии. Закон, которым она описывается, является достаточно простым: каждое следующее число отличается от предыдущего на множитель, который получил название "знаменатель". Можно обозначить его буквой r. Тогда можно записать следующее равенство:
Вам будет интересно:Многомировая интерпретация: теория Эверетта, история, возможность существования теории и мнения ученых
an+1 = an*r.
Здесь an - член прогрессии с номером n.
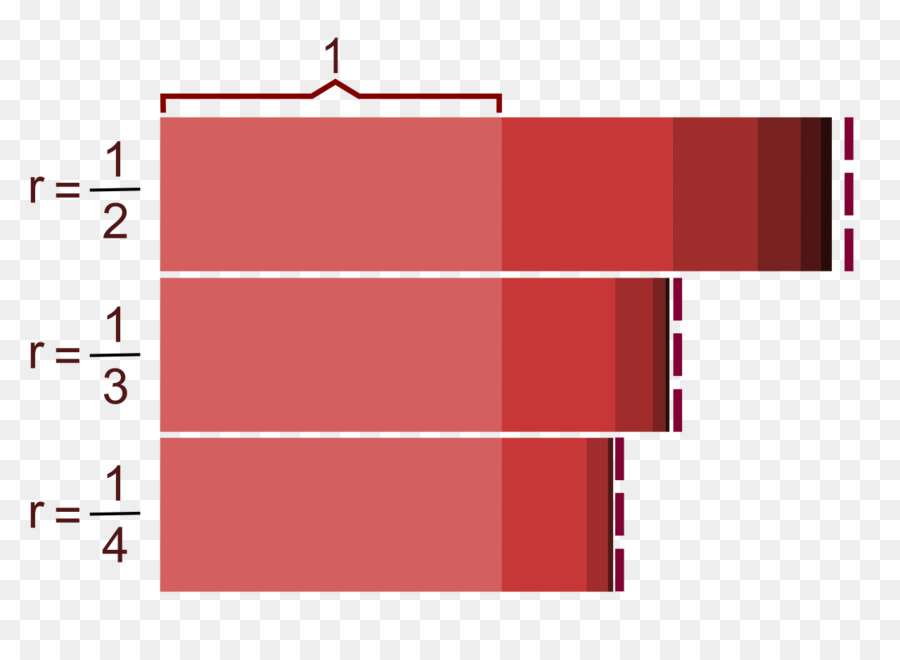
Если r будет больше 1, то прогрессия будет возрастать по модулю (она может убывать, если первый ее член будет иметь отрицательный знак). Если r будет меньше единицы, тогда вся прогрессия будет стремиться к нулю либо снизу (a1<0), либо сверху (a1>0). В случае отрицательного знаменателя (r<0) иметь место будет чередующаяся числовая последовательность (каждый положительный член будет окружен двумя отрицательными). Наконец, при равенстве r единице получится простой набор чисел, который, как правило, не называют прогрессией.
Пример рассматриваемого вида прогрессии приведен ниже:
2, 3, 4, 5, 6, 75, ...
Здесь первый член равен 2, а знаменатель равен 1,5.
Важные формулы
Как в 9 классе решать геометрическую прогрессию? Для этого следует знать не только ее определение и понимать, о чем идет речь, но и запомнить две важных формулы. Первая из них приводится ниже:
an = a1*rn-1.
Выражение позволяет без особого труда найти произвольный элемент последовательности, однако для этого необходимо знать два числа: знаменатель и первый элемент. Доказать эту формулу просто, нужно лишь вспомнить определение геометрической прогрессии: второй элемент получается умножением первого на знаменатель в первой степени, третий элемент - умножением первого на знаменатель во второй степени и так далее. Полезность этого выражения очевидна: нет необходимости в последовательном восстановлении всего числового ряда, чтобы узнать, какое значение примет его n-й элемент.
Следующая формула является также полезной при ответе на вопрос, как решать геометрическую прогрессию. Речь идет о сумме ее элементов, начиная с первого и заканчивая n-ным. Соответствующее выражение приведено ниже:
Sn = a1*(rn-1)/(r-1).
Стоит обратить внимание на его особенность: как и в формуле для нахождения n-ного элемента, здесь тоже достаточно знать те же два числа (a1 и r). Этот результат не является удивительным, ведь каждый член прогрессии связан с отмеченными числами.
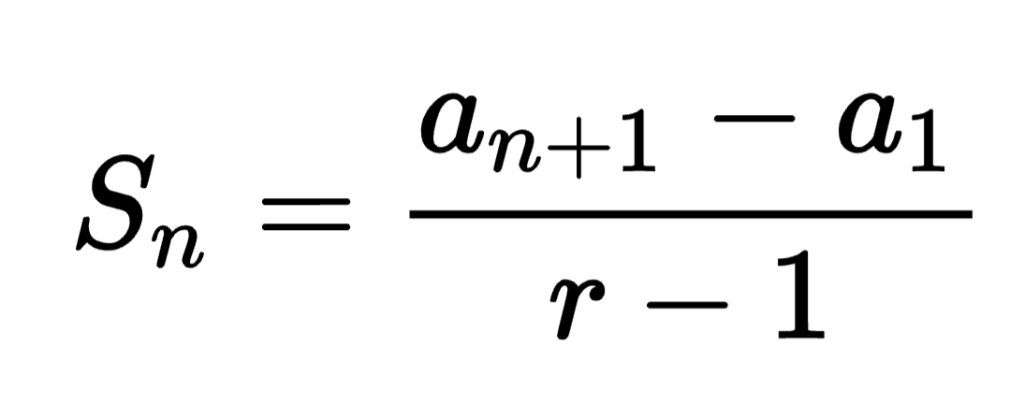
Далее приведено несколько примеров, в которых показано, как решить геометрическую прогрессию .
Восстановление прогрессии
Первый пример, как решать геометрическую прогрессию, имеет следующее условие: известно, что два числа 10 и 20 образуют рассматриваемый вид прогрессии. При этом числа являются восьмым и пятнадцатым элементами ряда. Необходимо восстановить весь ряд, зная, что он должен быть убывающим.
Это несколько запутанное условие задачи следует разобрать внимательно: поскольку речь идет об убывающем ряде, то число 10 должно стоять в 15 позиции, а 20 - в 8. Приступая к решению, выпишите для каждого из чисел соответствующие равенства:
a8 = a1*r7 и a15 = a1*r14.
Вы имеете два равенства с двумя неизвестными. Решите их, выражая из первого a1 и подставляя его во второе. Получится:
a1 = a8*r-7 и a15 = a8*r-7 *r14=a8*r7 => r=7√(a15/a8).
Теперь остается подставить соответствующие значения из условия и вычислить корень седьмой степени. Получится:
r=7√(a15/a8) = 7√(10 /20 ) ≈ 0,9057.
Подставляя полученный знаменатель в любое из выражений для известного n-ного элемента, получается a1:
a1 = a8*r-7 = 20*(0,9057)-7 ≈ 40,0073.
Таким образом, вы найдете первый член и знаменатель, что означает, что вы восстановите всю прогрессию. Первые несколько членов:
40,0073, 36,2346, 32,8177, 29,7230, ...
Стоит отметить, что при выполнении расчетов было использовано округление до 4-х знаков после запятой.
Нахождение неизвестного члена ряда
Теперь стоит рассмотреть иной пример: известно, что седьмой элемент ряда равен 27, чему равен тринадцатый член, если знаменатель r = -2. Как решить геометрическую прогрессию, пользуясь этими данными? Очень просто, нужно выписать формулу для 7-го элемента:
a7 = a1*r6.
Поскольку в этом равенстве неизвестно только число a1, выразите его:
a1 = a7*r-6.
Воспользуйтесь последним равенством, подставляя его в формулу для 13-го члена, который необходимо найти. Получится:
a13 = a1*r12 = a7*r-6*r12 = a7*r6.
Осталось подставить числа и записать ответ:
a13 = a7*r6 = 27*(-2)6 = 1728.
Полученное число демонстрирует, насколько быстро растет геометрическая прогрессия.
Задача на сумму
Последняя задача, раскрывающая вопрос, как решить геометрическую прогрессию, связана с нахождением суммы нескольких элементов. Пусть a1 = 1,5, r = 2. Следует вычислить сумму членов этого ряда, начиная с 5-го и заканчивая 10-м.
Чтобы получить ответ на поставленный вопрос, следует применить формулу:
S510 = S10 - S4.
То есть сначала нужно найти сумму 10 элементов, затем сумму первых 4-х и вычесть их между собой. Следуя указанному алгоритму, получится:
S10 = a1*(rn-1)/(r-1) = 1,5*(210-1)/(2-1) = 1534,5;
S4 = a1*(rn-1)/(r-1) = 1,5*(24-1)/(2-1) = 22,5;
S510 = 1534,5 - 22,5 = 1512.
Стоит отметить, что в конечной формуле вычиталась сумма именно 4 слагаемых, поскольку пятое по условию задачи должно участвовать в сумме.
