При математическом описании вращательного движения важно знать момент инерции системы относительно оси. В общем случае процедура нахождения этой величины предполагает реализацию процесса интегрирования. Облегчить вычисления позволяет так называемая теорема Штейнера. Рассмотрим ее подробнее в статье.
Что такое момент инерции?
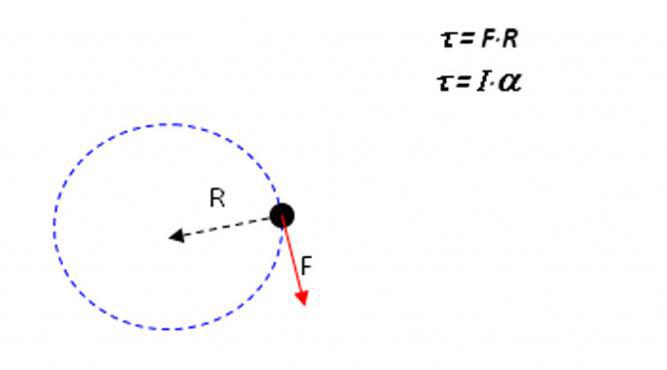
До того как привести формулировку теоремы Штейнера, следует разобраться с самим понятием момента инерции. Допустим, имеется некоторое тело определенной массы и произвольной формы. Этим телом может быть, как материальная точка, так и любой двумерный и трехмерный объект (стержень, цилиндр, шар и т.д.). Если рассматриваемый объект совершает круговое движение вокруг некоторой оси с постоянным угловым ускорением α, тогда можно записать следующее уравнение:
 Вам будет интересно:Анализ занятия воспитателя детского сада: пример, схема
Вам будет интересно:Анализ занятия воспитателя детского сада: пример, схема
M = I*α
Здесь величина M представляет суммарный момент сил, который придает ускорение α всей системе. Коэффициент пропорциональности между ними - I, называется моментом инерции. Эта физическая величина рассчитывается по следующей общей формуле:
I = ∫m (r2*dm)
Здесь r - это дистанция между элементом с массой dm и осью вращения. Это выражение означает, что необходимо найти сумму произведений квадратов расстояний r2 на элементарную массу dm. То есть момент инерции не является чистой характеристикой тела, что его отличает от линейной инерции. Он зависит от распределения массы по всему объекту, который вращается, а также от расстояния до оси и от ориентации тела относительно нее. Например, стержень будет иметь разный I, если его вращать относительно центра масс и относительно конца.
Момент инерции и теорема Штейнера

Известный швейцарский математик, Якоб Штейнер, доказал теорему о параллельных осях и моменте инерции, которая теперь носит его фамилию. Эта теорема постулирует, что момент инерции для абсолютно любого твердого тела произвольной геометрии относительно некоторой оси вращения равен сумме момента инерции относительно оси, которая пересекает центр масс тела и параллельна первой, и произведения массы тела на квадрат дистанции между этими осями. Математически эта формулировка записывается так:
IZ = IO + m*l2
IZ и IO - моменты инерции относительно оси Z и параллельной ей оси O, которая проходит через центр масс тела, l - расстояние между прямыми Z и O.
Теорема позволяет, зная величину IO, рассчитать любой другой момент IZ относительно оси, которая параллельна O.
Доказательство теоремы
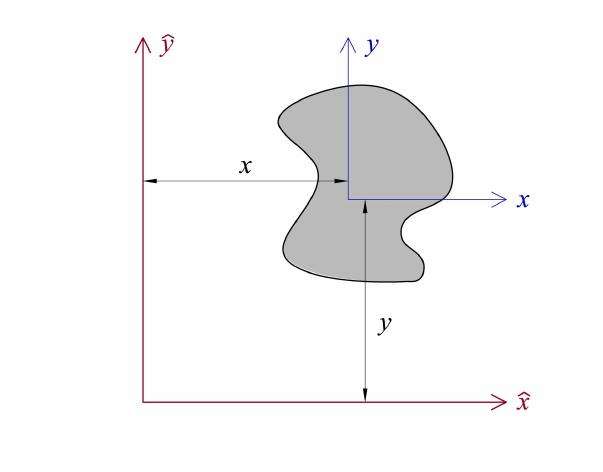
Формулу теоремы Штейнера можно легко получить самостоятельно. Для этого рассмотрим произвольное тело на плоскости xy. Пусть начало координат проходит через центр масс этого тела. Рассчитаем момент инерции IO которая проходит через начало координат перпендикулярно плоскости xy. Поскольку расстояние до любой точки тела выражается формулой r = √ (x2 + y2), тогда получаем интеграл:
IO = ∫m (r2*dm) = ∫m ( (x2+y2) *dm)
Теперь переместим параллельно ось вдоль оси x на расстояние l, например, в положительном направлении, тогда расчет для новой оси момента инерции будет выглядеть следующим образом:
IZ = ∫m (( (x+l)2+y2)*dm)
Раскроем полный квадрат в скобках и разделим подынтегральные суммы, получим:
IZ = ∫m ( (x2+l2+2*x*l+y2)*dm) = ∫m ( (x2+y2)*dm) + 2*l*∫m (x*dm) + l2*∫mdm
Первое из этих слагаемых является величиной IO, третье слагаемое, после проведения интегрирования, дает член l2*m, а вот второе слагаемое равно нулю. Обнуление указанного интеграла связано с тем, что он берется от произведения иксов на элементы массы dm, что в среднем дает ноль, так как центр масс находится в начале координат. В итоге, получается формула теоремы Штейнера.
Рассмотренный случай на плоскости можно обобщить на объемное тело.
Проверка формулы Штейнера на примере стержня
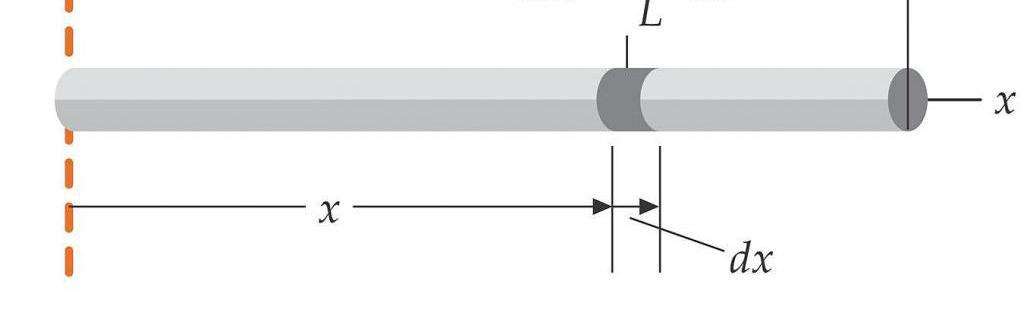
Приведем простой пример, на котором продемонстрируем, как пользоваться рассмотренной теоремой.
Известно, что для стержня длиной L и массой m момент инерции IO (ось проходит через центр масс) равен m*L2/12, а момент IZ (ось проходит через конец стержня) равен m*L2/3. Проверим эти данные, воспользовавшись теоремой Штейнера. Поскольку расстояние между двумя осями равно L/2, тогда получаем момент IZ:
IZ = IO + m*(L/2)2 = m*L2/12 + m*L2/4 = 4*m*L2/12 = m*L2/3
То есть мы проверили формулу Штейнера и получили такое же значение для IZ, что и в источнике.
Аналогичные вычисления можно проводить и для других тел (цилиндра, шара, диска), получая при этом необходимые моменты инерции, и не производя интегрирования.
Момент инерции и перпендикулярные оси
Рассмотренная теорема касается параллельных осей. Для полноты информации полезно также привести теорему для перпендикулярных осей. Она формулируется так: для плоского объекта произвольной формы момент инерции относительно перпендикулярной ему оси будет равен сумме двух моментов инерции относительно двух взаимно перпендикулярных и лежащих в плоскости объекта осей, при этом все три оси должны проходить через одну точку. Математически это записывается так:
Iz = Ix + Iy
Здесь z, x, y - три взаимно перпендикулярные оси вращения.
Существенное отличие этой теоремы от теоремы Штейнера заключается в том, что она применима только к плоским (двумерным) твердым объектам. Тем не менее на практике ее достаточно широко используют, мысленно разрезая тело на отдельные слои, а затем, складывая полученные моменты инерции.
