Окружность и круг - две совершенные плоские фигуры, свойства которых изучают в обязательном порядке в любом школьном курсе геометрии. В этой статье мы рассмотрим, как находить длину окружности и площадь круга, используя простые математические формулы.
В чем разница между окружностью и кругом?
Прежде чем переходить к рассмотрению формул длины окружности и площади круга, следует привести определения этих фигур.
В геометрии под окружностью понимают совокупность точек на плоскости, которые находятся от фиксированной точки на одинаковом расстоянии R. В свою очередь, круг - это набор точек плоскости, которые от заданной точки расположены на расстояниях, равных или меньших, чем некоторое число R. Иными словами, окружность представляет собой одну единственную кривую линию, а круг занимает некоторую площадь. Окружность - это "обод" круга.
 Вам будет интересно:Династия Шан: основоположник, исторические факты
Вам будет интересно:Династия Шан: основоположник, исторические факты
Именно поэтому, вопрос, как находить площадь окружности, считается некорректно поставленным. Окружность (единственная линия) не имеет площади, однако имеет длину. Для круга же разговор о площади имеет смысл, кроме того, также можно говорить и о длине окружности, которая его ограничивает.
Основные свойства рассматриваемых фигур
Окружность и круг обладают рядом общих характеристик, которые кратко перечислим ниже:
Формулы для длины окружности и площади круга
Познакомившись с понятием и основными свойствами рассматриваемых плоских фигур, можно перейти к количественному определению их размеров. Длина окружности и площадь круга вычисляются по следующим двум формулам:
1. L = 2 * π * R.
2. S = π * R²
Из этих формул следует, что величина R - радиус - полностью характеризует свойства обеих фигур. Величина L измеряется в метрах (~R), а S - в метрах квадратных (~R²).
В формулах символ π представляет некоторую константу, которая является иррациональным числом (ее нельзя вычислить точно). С точностью до 4 знаков после запятой число π равно 3,1416. Отметим, что при выполнении расчетов эта константа может быть заменена дробью 201/64. Если вычислить значение этой дроби, то получится число 3,1406, которое всего на 0,03 % отличается от истинной константы.
Заметим, что формула для длины окружности справедлива также для определения аналогичной характеристики круга.
Указанные формулы могут быть переписаны через диаметр, учитывая, что D = 2 * R, получаем:
1) L = π * D;
2) S = π * D²/4.
Использование рассмотренных формул для решения задачи
Формулы для площади круга и длины окружности используем для решения задач. Например, у Маши имеется кусок ткани прямоугольной формы, размеры которой равны 5 x 4 метра. Необходимо определить, какого максимального размера круг она сможет вырезать из этой ткани.
Смысл этой задачи состоит в определении размера круга, вписанного в четырехугольник. Эта ситуация изображена на рисунке ниже.
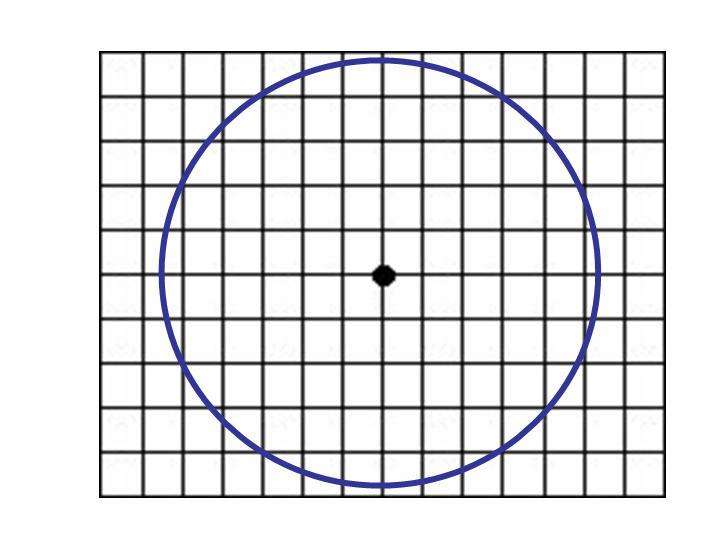
Из рисунка можно заметить, что диаметр вписанного круга D будет равен длине наименьшей стороны четырехугольника, в данном случае D = 4 метра. Зная диаметр, можно непосредственно применить формулы, которые записаны для длины и площади этой фигуры в предыдущем пункте статьи. Имеем:
1. L = π * D = 3,1416 * 4 = 12,5664 м.
2. S = π * D²/4 = 3,1416 * 4²/4 = 12,5664 м².
Мы получили любопытный результат: площадь круга равна точно такой же величине, что и длина его окружности, но единицы измерения являются разными для них. Этот результат является простым совпадением, поскольку D=4 - это единственное число, для которого абсолютные значения L и S равны.

