Когда в общеобразовательных школах изучают свойства упорядоченных последовательностей чисел, то в обязательном порядке рассматривают так называемую убывающую бесконечную геометрическую прогрессию. Раскроем подробнее этот вопрос в статье.
Что такое геометрическая прогрессия?
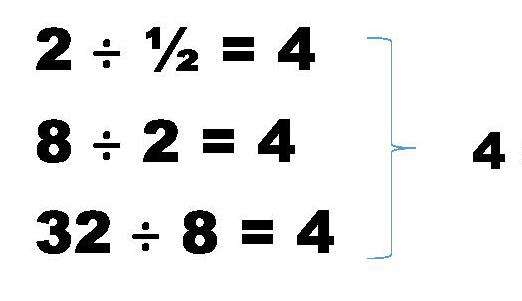
Перед тем как переходить к объяснению убывающей бесконечной геометрической прогрессии, следует дать определение этой числовой последовательности. Прогрессия геометрическая - это такой ряд чисел, в котором любой последующий член однозначно получается из предыдущего путем умножения его на некоторое рациональное число. Это число называется знаменателем.
Вам будет интересно:Future in the Past: правила речи, склонение, время, понятие, определения, особенности изучения и нюансы произношения
Примером этого вида прогрессии является следующий ряд чисел: 1, 4, 16, 64, ... Видно, что если умножить любое из этих чисел на 4, то получается следующий член ряда. Это означает, что знаменатель этой последовательности находится по формуле: r = an/an-1, здесь an и an-1 - n-й и (n-1)-й члены прогрессии.
Исходя из определения этого вида прогрессии, можно n-й ее член найти, используя следующее выражение: an = a1*r(n-1), то есть достаточно знать знаменатель и первый член числового ряда.
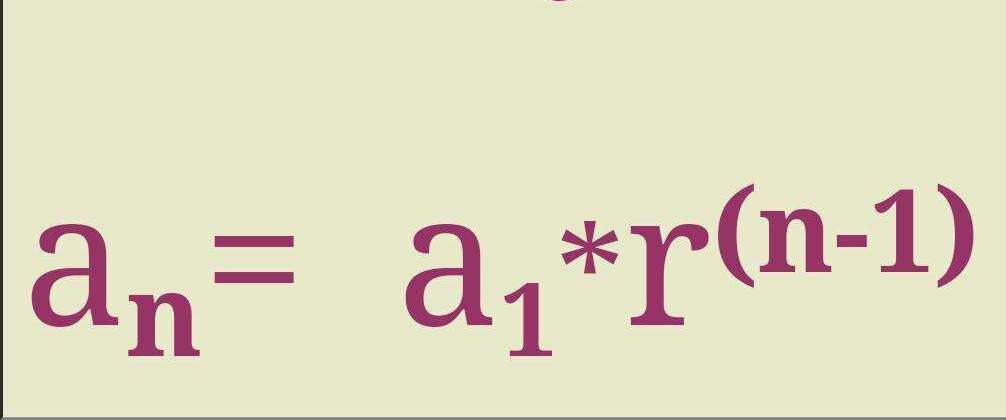
Например, найдем 8-е число в геометрической прогрессии, приведенной выше. Имеем: a8 = a1*r7 = 1*47 = 16384.
Еще одной важной формулой для геометрической прогрессии является выражение для нахождения суммы ее n первых членов. Эта формула имеет вид: Sn = a1*(rn-1)/(r-1). Применим ее для нахождения суммы 8-ми чисел из последовательности выше. Получаем: S8 = 1*(48-1)/(4-1) = 21845.
Какие бывают геометрические прогрессии
В зависимости от знака и модуля знаменателя r выделяют 4 вида геометрической прогрессии:
- Возрастающая. Если r>1, тогда каждый последующий член будет больше предыдущего по модулю. Бесконечная сумма такого ряда стремится к бесконечности (или минус бесконечности, если 1-й член является отрицательным числом). Пример этой прогрессии рассмотрен в предыдущем пункте.
- Постоянная. Если r=1, то мы имеем обычный набор одинаковых чисел.
- Переменная. Если r<0 и |r|>1, то мы получаем последовательность, в которой два соседних члена отличаются по знаку. Например, 1, -3, 9, -27, 81, ... Здесь r = -3.
- Убывающая. Если |r|<1, то с увеличением номера числа в ряду будет уменьшаться его абсолютное значение. Следующий ряд является ярким примером этого вида геометрической прогрессии: 100, 50, 25, 12,5 ..., где знаменатель r = 0,5.
Далее в статье рассмотрим убывающую прогрессию как наиболее интересный и полезный для практики числовой ряд.
Убывающая прогрессия
Как было сказано выше, знаменатель убывающей бесконечно прогрессии геометрической по модулю должен быть меньше единицы, то есть |r|<1. Это означает, что он может быть как положительным, так и отрицательным.
Практический интерес представляет сумма членов прогрессии геометрической бесконечно убывающей, потому что она представляет собой некоторое конечное число.
Чтобы получить формулу для рассматриваемого случая, воспользуемся выражением для суммы, которое приведено в первом пункте статьи: Sn = a1*(rn-1)/(r-1). Если рассматривать бесконечный ряд, то есть n>∞, тогда rn>0, поскольку |r|<1. Этот факт можно проверить, если взять любое число, удовлетворяющее последнему условию, и возвести его в большую степень. В результате формула для суммы n слагаемых при n>∞ для убывающей прогрессии примет вид: S∞ = a1*/(1-r).
Приведем пример использования полученной формулы. Пусть необходимо найти бесконечную сумму для ряда 100, 50, 25, 12,5 ... Как видно, первый член прогрессии геометрической убывающей бесконечно a1 равен 100, а ее знаменатель r = 0,5 (50/100 = 25/50 = 12,5/25). Подставим эти значения в формулу для бесконечной суммы, получим: S∞ = a1*/(1-r) = 100/(1-0,5) = 200.
Черепаха и Ахиллес (парадокс Зенона)
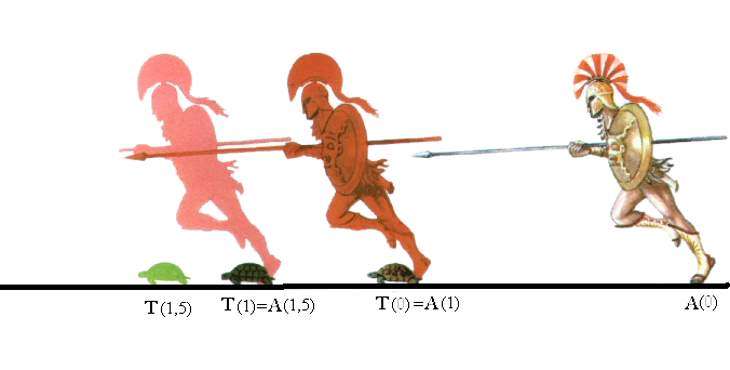
Где можно использовать результат, полученный в пункте выше? Например, при объяснении парадокса древнегреческого философа Зенона. Суть этого парадокса заключается в том, что Ахиллес (с древнегреческого языка это имя переводится, как "тот, кто обладает "легкими" ногами"), будучи самым быстрым воином, не может догнать черепаху.
Зенон рассуждал следующим образом: если черепаха будет впереди Ахиллеса, и они одновременно начнут движение, то когда воин достигнет места, откуда взяла старт черепаха, последняя уже отползет на некоторое расстояние, поэтому Ахиллесу придется снова его преодолевать (хотя оно и меньше, чем первоначальное). Пробежав новый отрезок пути, воин все равно окажется позади черепахи, ведь она опять проползет некоторую дистанцию. Так способом можно рассуждать до бесконечности.
Каждый из нас знает, что не только Ахиллес, но и любой человек, двигаясь пешком, обгонит черепаху. В чем же ошибся философ? Он не учел, что хотя сумма отрезков является бесконечной, она приводит к конечному числу S∞. Как только Ахиллес преодолеет расстояние S∞, он сразу же обгонит черепаху.
Любопытно отметить, что сам философ объяснял тот факт, что Ахиллес на практике все же обгоняет черепаху, тем, что движение и время являются иллюзией, и в реальности не существуют.
